 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Організація циклів для доступу до елементів, розташованих у визначених частинах масиву
Під час розв’язування задач на обробку квадратних матриць часто виникає необхідність розглядати не всі елементи, а лише їх певну частину. Наведемо приклади організації циклів для доступу до елементів, що знаходяться в певних частинах матриці.
Приклад 1. Нижче від головної діагоналі:

| дляі від 1 до n пц для j від 1 до і пц серія кц кц | for i:=1 to n do for j:=1 to i do begin < серія > end; |
Приклад 2. Найвище від головної діагоналі:

| для і від 1 до n пц для j від і до n пц серія кц кц | for i:=1 to n do for j:=i to n do begin < серія > end; |
Приклад 3. Найвище від побічної діагоналі:
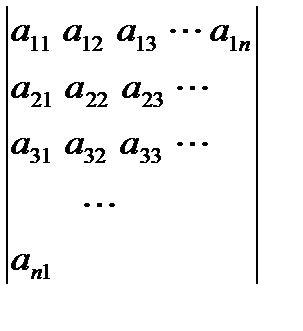
| для і від 1 до n пц для j від 1 до n+1-і пц серія кц кц | for i:=1 to n do for j:=1 to n+1 – i do begin < серія > end; |
Приклад 4. Найнижче від побічної діагоналі:
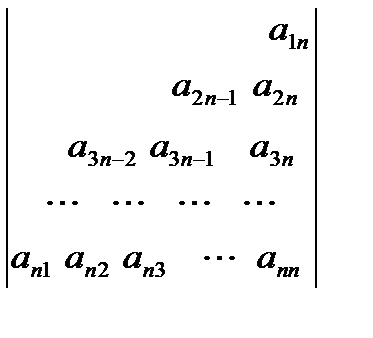
| для і від 1 до n пц для j від n+1 – i до n пц серія кц кц | for i:=1 to n do for j:=n+1 – i to n do begin < серія > end; |
Приклад 5. У таких областях:
а) 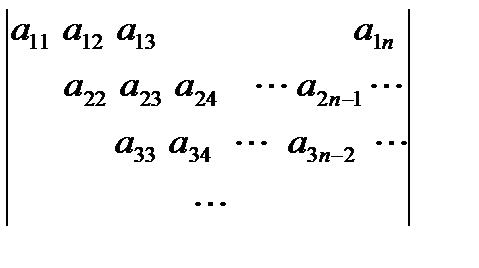
| для і від1 до int (n/2+0.5) пц для j від і до n+1 – і пц серія кц кц | fori:=1 to (n+1) div 2 do for j:=1 to n+1 – i do begin < серія > end; |
б) 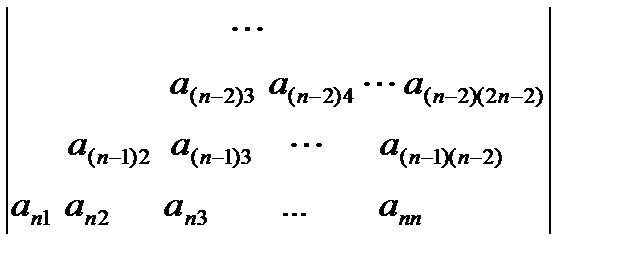
| для і від int(n/2+0.5) до n пц для j від n+1 - і до і пц серія кц кц | for i:=(n+1) div 2 to n do for j:=n+1 – i to i do begin < серія > end; |
в) 
| для j від 1 до int(n/2+0.5) пц для і від j до n+1 – j пц серія кц кц | for j:=1 to (n+1) div 2 do for i:=j to n+1 – j do begin < серія > end; |
г) 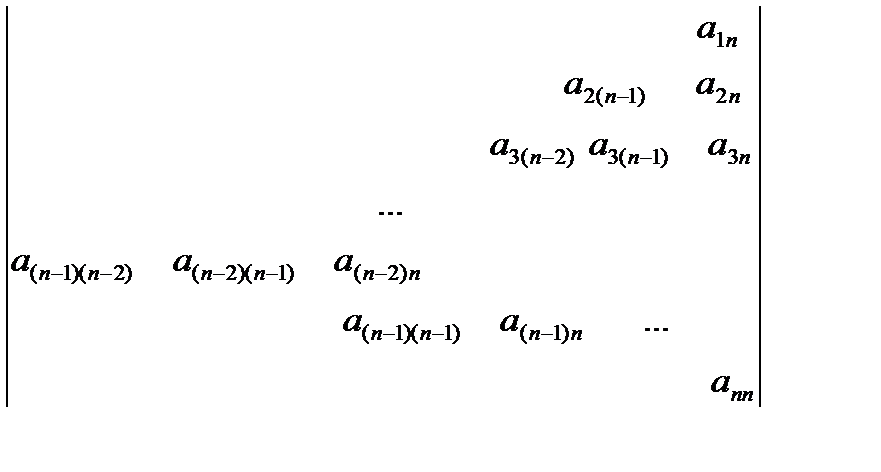
| для j від int(n/2+0.5) до n пц для і від n+1 – j до j пц серія кц кц | for j:=(n+1) div 2 to n do for i:=n+1 – j to j do begin < серія > end; |
ОБЛАСТІ У ПРИКЛАДІ 5 МАЮТЬ ФОРМУ ТРИКУТНИКА АБО ТРАПЕЦІЇ, ЗАЛЕЖНО ВІД ТОГО, ПАРНЕ АБО НЕПАРНЕ ЧИСЛО n (порядок матриці). ЯКЩО n – ПАРНЕ, ТО ФОРМА ОБЛАСТІ МАЄ ВИГЛЯД ТРАПЕЦІЇ, ІНАКШЕ – ТРИКУТНИКА!
Приклад 6. Для роботи з елементами головної діагоналі досить одного циклу, оскільки i=j, тому для доступу до будь-якого елемента варто вказувати в циклі A[i, i].

| для і від 1 до n пц серія кц | for i:=1 to n do begin < серія > end; |
Приклад 7. Для роботи з елементами побічної діагоналі також досить одного циклу, тому що і зростає (від 1 до n), а j – спадає (від n до 1), тому для доступу до будь-якого елемента варто вказувати в циклі A[i, n+1 – i].

| дляі від 1 до n пц серія кц | for i:=1 to n do begin < серія > end; |
Для доступу до елементів матриці можна використовувати умови: i=j – елементи головної діагоналі; i+j=n+1 – елементи побічної діагоналі; i>j – елементи, що знаходяться нижче від головної діагоналі; i<j – елементи, що знаходяться вище від головної діагоналі. Але в цьому випадку необхідно переглядати всі елементи матриці.
Наведемо вправи на організацію циклів для доступу до елементів, що знаходяться у зазначених частинах матриці.
Вправи
Вправа 1. Дано матрицю порядку n. Знайдіть, де більше максимальних елементів – на головній діагоналі або бічній. Видати ці елементи і їхню кількість.
Наведемо два варіанти розв’язування цієї вправи.
Алгоритм має вигляд:
Поиск по сайту: