 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Пояснення до алгоритму
1.Якщо числа рівні, то взяти кожне з них як результат, інакше продовжити виконання алгоритму.
2.Визначити більше число з двох чисел і замінити більше число різницею більшого й меншого чисел; почати алгоритм спочатку.
Запропонований алгоритм не викликає сумнівів, але не є оптимальним у такому випадку, коли одне з чисел набагато більше від другого, наприклад, 11 та 10111. Більш показовою є пара чисел 5 та 10 000. Очевидно, що 5 – це їх найбільший спільний дільник, але результат ми отримуємо після майже 2000 занурень у рекурсію (саме стільки необхідно зробити віднімань, щоб числа стали рівними).
Щоб оптимізувати алгоритм, пропонуємо замінити віднімання цілочисельним діленням. Остачею від ділення будемо замінювати більше з чисел, процес закінчиться, коли числа стануть рівними – це і є їх найбільший спільний дільник.
Мовою Паскаль це записується так:
while a mod b<>0 do
Begin
A:=a mod b;
c:=a; a:=b; b:=c;
end;
тобто поки а не поділиться на b націло, записуємо b, а залишок від ділення а на b, а потім міняємо місцями а та b, оскільки а після заміни обов’язково буде менше b (залишок завжди менше дільника).
Оформимо тепер цей алгоритм рекурсивно. Отже, вихід з рекурсії відбудеться, якщо остачу від ділення а на b дорівнюватимемо 0, а занурення – у протилежному випадку.
Function NSD (a, b: longint): longint;
Begin
if a mod b=0
then NSD:=b
else a:=NSD (b, a mod b)
end;
Приклад 5. Знайти суму цифр натурального числа.
Рекурсивне визначення функції sumc(n) – суми цифр натурального числа n – має вигляд:

Алгоритм-функція sumc(n) має вигляд:
| Мовою НАМ: | Мовою Паскаль: |
| АЛГ ціл sumc(n) (ціл n) ПОЧ ціл і, m якщо n=0 то sumc:=0 інакше sumc:=n mod 10 + sumc(n div 10) все КІН | FunctionSum_cifra (n:longint):byte; begin if n=0 then Sum_cifra:=0 else Sum_cifra:=n mod 10+Sum_cifra(n div 10); end; |
Словесно це можна сформулювати таким чином: сума цифр n -цифрового числа дорівнює сумі останньої цифри цього числа (n mod 10) та сумі цифр (n – 1)-цифрового числа (Sum_cifra:=n div 10).
Приклад 6. Задача про Ханойські вежі. Є три стрижні А, В, С і n дисків різних діаметрів, які можна нанизувати на стрижні. Спочатку всі диски розташовані на одному стрижні (наприклад, А ) за зростанням їхніх діаметрів (діаметр нижнього диска більший від діаметра верхнього). Необхідно перемістити всю піраміду на інший стрижень ( В ), використовуючи допоміжний третій стрижень С і виконуючи при цьому правила:
1) за один хід можна перекласти тільки один диск;
2) диск більшого діаметра не можна класти на диск меншого діаметра.
Завдання полягає у визначенні послідовності переміщення дисків для перенесення їх із стрижня А на стрижень В.
Розв’язання. При n=1 розв’язання завдання можна подати у вигляді А-А – В. При n=2 завдання також легко вирішується: А-А – С, А-А – В, С-С – В. Уже під час розв’язання завдання при n=3 ми можемо побачити закономірність переміщення кілець: спочатку необхідно перемістити n – 1 дисків, що лежать на нижньому диску стрижня А, на стрижень С (рис. 2), потім виконати переміщення А-А – В (найближчого диска) і, нарешті, перемістити (n – 1) дисків із стрижня С на В, використовуючи стрижень А.

Легко помітити, що схема опису дій для розв’язання завдання виявилася рекурсивною. Запишемо отримане рекурсивне формулювання завдання:
Перемістити n дисків з А на В, використовуючи С
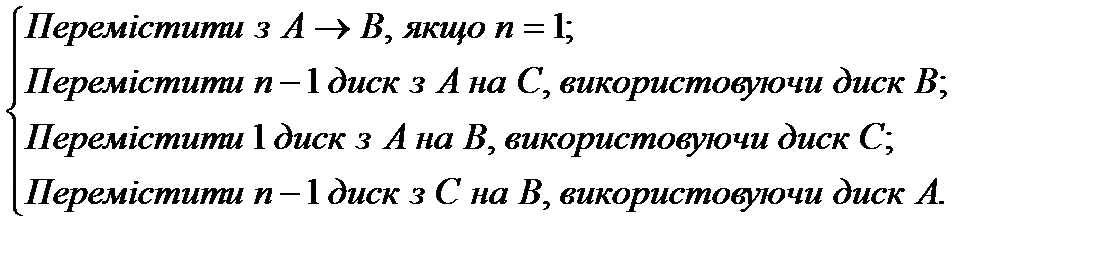
Повне розв’язання завдання, головний і рекурсивний алгоритми, наводяться нижче.
| Головний алгоритм має вигляд: | Рекурсивний алгоритм HANOY має вигляд: |
| АЛГ Головний (ціл n) АРГ n ПОЧ літ А, В, С A:=’A’; B:=’B’; C:=’C’ HANOY(n, A, B, C) КІН | АЛГHANOY (ціл n, літ А, В, С) АРГ n, A, B, C ПОЧ якщо n=1 то ДРУКУВАТИ(A, ‘->’, B) {перекласти 1 диск з А на В} інакше HANOY(n – 1, A, C, B) HANOY(1, A, B, C) HANOY(n – 1, C, B, A) все КІН |
Якщо ми змогли б перенести n – 1 диск з початкового стрижня А на стрижень С, використовуючи стрижень В як допоміжний, то останній диск легко перекласти на стрижень В. Після цього аналогічними міркуваннями переносимо n – 1 диск із стрижня С на стрижень В, використовуючи стрижень А як допоміжний, тобто
Поиск по сайту: