Матрицы. Матрицей размера называется прямоугольная таблица из чисел ( ,

Матрицей размера называется прямоугольная таблица из чисел (, ): , состоящая из строк и столбцов. Если необходимо указать размеры матрицы, то пишут .

Если , то матрица называется квадратной.

Нулевой называется матрица , все элементы которой равны нулю, например: . Единичной называется квадратная матрица , на главной диагонали которой стоят единицы, а все остальные элементы равны нулю, например: . Треугольной называется квадратная матрица , все элементы которой расположенные по одну сторону от главной диагонали равны нулю, например: . Трапециевидной (ступенчатой) называется матрица , все элементы которой, расположенные ниже элементов равны нулю, например: .

Матрицы и называются равными и пишут , если они одинакового размера и их соответствующие элементы равны: , , .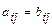

Матрицы можно транспонировать, складывать, вычитать, умножать на число, умножать на другую матрицу.

Транспонированной к матрице называется матрица , столбцами которой являются соответствующие строки матрицы .

Суммой (разностью) матриц и одного размера , называется матрица того же размера, для которой:

, , .

Произведением матрицы размера на число называется матрица того же размера, для которой: , , .

Линейной комбинацией матриц и одного размера , называется матрица того же размера ( и - произвольные числа), для которой: , , ,

Произведением матрицы на матрицу называется матрица , каждый элемент которой вычисляется по правилу:

, , .

Операция умножения матрицы на матрицу определена не для всех матриц, а только для таких у которых число столбцов левой матрицы равно числу строк правой матрицы . Такие матрицы называются согласованнымидля умножения. Поэтому прежде чем выполнять операцию умножения матрицы на матрицу следует проверить их согласованность для умножения и определить размерность матрицы-произведения (если умножение матриц возможно): . Особенность операции умножения матриц состоит в том, что в общем случае: , т.е. переместительное свойство места не имеет.

Элементарными преобразованиями матрицы называются:

1) перестановка строк (столбцов);

2) умножение строки (столбца) на число, отличное от нуля;

3) прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число;

4) вычёркивание нулевой строки (столбца).

Матрицы и , полученные одна из другой в результате элементарных преобразований называются эквивалентными и пишут .

Обратной к квадратной матрице порядка , называется матрица того же порядка, если: , где - единичная матрица порядка .

Квадратная матрица называется невырожденной, если её определитель . Обратная матрица всегда существует для невырожденных матриц.

Основными методами вычисления обратной матрицы являются:

Метод присоединённой матрицы. Если -невырожденная матрица, то , где - присоединённая матрица, для которой: . Здесь - алгебраические дополнения элементов матрицы .

В частности, если , то

Метод элементарных преобразований. Для данной квадратной матрицы порядка строится прямоугольная матрица размера приписыванием к справа единичной матрицы. Далее, с помощью элементарных преобразований над строками, матрица приводится к виду , что всегда возможно, если - невырожденная.

Матричными называются уравнения вида: , , ,

где матрицы - известны, матрица - неизвестна. Если квадратные матрицы и - невырожденные, то решения матричных уравнений записываются, соответственно, в виде: , , .

Минором -ого порядка матрицы размера называется определитель квадратной матрицы порядка , образованной элементами матрицы , стоящими на пересечении произвольно выбранных её строк и столбцов .

Максимальный порядок отличных от нуля миноров матрицы , называется её рангом и обозначается или , а любой минор порядка , отличный от нуля – базисным минором.

Поиск по сайту: