АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение

Читайте также:
  1. Волновое уравнение для упругих волн и его общее решение.
  2. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  3. Дифференциальное уравнение вынужденных колебаний и его решение. Резонанс. Резонансные кривые.
  4. Дифференциальное уравнение затухающих колебаний и его решение. Основные характеристики затухающих колебаний. Логарифмический декремент затухания. Апериодический процесс.
  5. Рациональное управленческое решение. Способы принятия рационального решения. Списки. Дерево решений. Причинно-следственные диаграммы.
  6. Решение.
  7. Решение.
  8. Решение.
  9. Решение.
  10. Решение.
  11. Решение.
  12. Решение.

1а) Вычисляем : .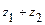

2а) Вычисляем .

Сначала находим (учитываем, что ) . Тогда

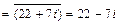
3а) Вычисляем :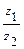

(учитываем, что ) .

1б) Представляем комплексное число в тригонометрической форме , где

(так как комплексное число, изображается точкой 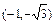, лежащей в третьем квадранте координатной плоскости). Тогда .

2б) Вычисляем по формуле Муавра:

. Полученный результат представляем в алгебраической форме: .

1в) Для нахождения корней алгебраического уравнения , раскладываем его левую часть на множители:

.

2в) Находим корни уравнения на множестве комплексных чисел, приравнивая каждый из множителей нулю (число корней, с учётом кратности, должно равняться порядку уравнения):

1) .

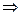
2) .

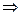
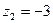3) . Так как дискриминант квадратного уравнения , то уравнение имеет два комплексно-сопряжённых корня: .

Замечание. Корни , можно найти и как корни уравнения 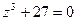, по формуле . Для нахождения комплексных значений корня, число следует представить в виде комплексного числа в тригонометрической форме: , после чего значения корня найти по формуле: ,где

Ответ: a) , , ;

б) ; в) , , .


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |

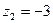Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)