Прямые линии и плоскости

Нормальным вектором прямой 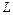, называется всякий ненулевой вектор перпендикулярный данной прямой. Направляющим вектором прямой 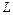, называется всякий ненулевой вектор параллельный данной прямой.

Прямая 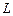на плоскости в системе координат может быть задана уравнением одного из следующих видов:

1) - общее уравнение прямой, где - нормальный вектор прямой;

2) - уравнение прямой, проходящей через точку перпендикулярно данному вектору ;

3) - уравнение прямой, проходящей через точку параллельно данному вектору (каноническое уравнение);

4) - уравнение прямой, проходящей через две данные точки , ;

5) -уравнения прямой с угловым коэффициентом , где - точка через которую прямая проходит; () – угол, который прямая составляет с осью ; - длина отрезка (со знаком ), отсекаемого прямой на оси (знак «», если отрезок отсекается на положительной части оси и «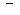», если на отрицательной).

6) -уравнение прямой в отрезках, где и - длины отрезков (со знаком ), отсекаемых прямой на координатных осях и (знак «», если отрезок отсекается на положительной части оси и «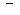», если на отрицательной).

Расстояние от точки до прямой 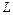, заданной общим уравнением на плоскости, находится по формуле:

.

Угол , () между прямыми и , заданными общими уравнениями или уравнениями с угловым коэффициентом, находится по одной из следующих формул:

; .

, если или .

,если или

Координаты точки пересечения прямых и находятся как решение системы линейных уравнений: или .

Нормальным вектором плоскости , называется всякий ненулевой вектор перпендикулярный данной плоскости.

Плоскость в системе координат может быть задана уравнением одного из следующих видов:

1) - общее уравнение плоскости, где 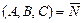- нормальный вектор плоскости;

2) - уравнение плоскости, проходящей через точку перпендикулярно данному вектору ;

3) - уравнение плоскости, проходящей через три точки , и ;

4) -уравнение плоскости в отрезках, где , и - дины отрезков (со знаком ), отсекаемых плоскостью на координатных осях , и 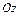(знак «», если отрезок отсекается на положительной части оси и «», если на отрицательной).

Расстояние от точки до плоскости , заданной общим уравнением , находится по формуле:

.

Угол , () между плоскостями и , заданными общими уравнениями, находится по формуле:

.

, если

, если .

Прямая 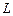в пространстве в системе координат может быть задана уравнением одного из следующих видов:

1) 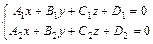- общее уравнение прямой, как линии пересечения двух плоскостей, где и - нормальные векторы плоскостей и ;

2) - уравнение прямой, проходящей через точку параллельно данному вектору (каноническое уравнение);

3) - уравнение прямой, проходящей через две данные точки , ;

4) -уравнение прямой, проходящей через точку параллельно данному вектору 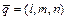, 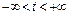(параметрическое уравнение);

Угол , () между прямыми и в пространстве, заданными каноническими уравнениями находится по формуле:

.

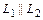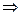
, если .

, если .

Координаты точки пересечения прямой 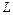, заданной параметрическим уравнением и плоскости , заданной общим уравнением, находятся как решение системы линейных уравнений: .

Угол , () между прямой 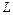, заданной каноническим уравнением и плоскостью , заданной общим уравнением находится по формуле: .

, если .

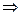
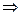
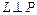, если .

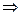
Поиск по сайту: