 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Решение. а)Длинырёбер и находим как длины векторов и
а) Длинырёбер  и
и  находим как длины векторов
находим как длины векторов 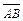 и
и 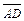 :
:
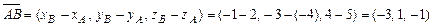 ;
;
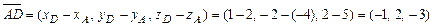 ;
;
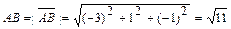 ;
;
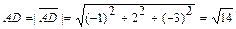 .
.
б) Угол 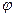 между рёбрами
между рёбрами  и
и  находим как угол между векторами
находим как угол между векторами 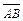 и
и 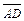 по формуле:
по формуле: 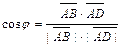 . Учитывая, что:
. Учитывая, что: 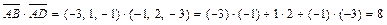 ,
, 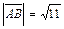 ,
, 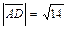 получим
получим 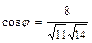 . Откуда
. Откуда 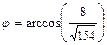
в) Площадь 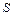 грани
грани  находим, используя геометрический смысл векторного произведения векторов, по формуле
находим, используя геометрический смысл векторного произведения векторов, по формуле 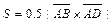 . Учитывая, что:
. Учитывая, что: 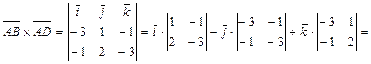
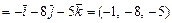 ,
, 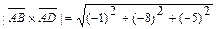 , получим
, получим 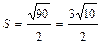 .
.
г) Объём  пирамиды
пирамиды  находим, используя геометрический смысл смешанного произведения векторов, по формуле
находим, используя геометрический смысл смешанного произведения векторов, по формуле 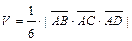 . Учитывая, что:
. Учитывая, что:
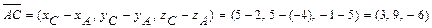 ,
,
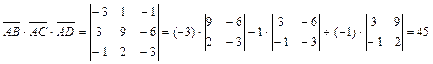 ,
,
получим 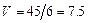 .
.
д) Уравнение плоскости грани  находим как уравнение плоскости, проходящей через точки
находим как уравнение плоскости, проходящей через точки 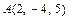 ,
, 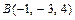 и
и 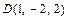 , и записываем его в виде общего уравнения плоскости:
, и записываем его в виде общего уравнения плоскости:
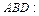
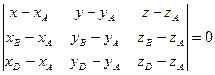
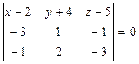
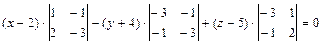

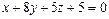
е) Длину  высоты
высоты  пирамиды
пирамиды  находим как расстояние от точки
находим как расстояние от точки 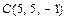 до плоскости
до плоскости  , заданной общим уравнением
, заданной общим уравнением 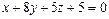 :
:
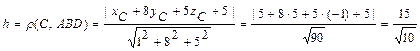 .
.
Ответ: а) 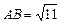 ,
, 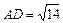 ; б)
; б) 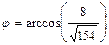 ; в)
; в) 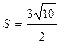 ;
;
г) 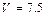 ; д)
; д) 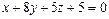 ; е)
; е) 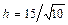 .
.
9. Даны комплексные числа 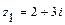 ,
, 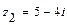 ,
,  и алгебраическое уравнение
и алгебраическое уравнение  . Требуется: а) вычислить
. Требуется: а) вычислить 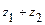 ,
,  ,
, 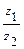 ; б) представить комплексное число
; б) представить комплексное число 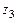 в тригонометрической форме, вычислить
в тригонометрической форме, вычислить  и результат представить в алгебраической форме; в) найти все корни алгебраического уравнения на множестве комплексных чисел.
и результат представить в алгебраической форме; в) найти все корни алгебраического уравнения на множестве комплексных чисел.
Поиск по сайту: