АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Решение. 1а)Записываем расширенную матрицу системы:

Читайте также:
  1. Волновое уравнение для упругих волн и его общее решение.
  2. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  3. Дифференциальное уравнение вынужденных колебаний и его решение. Резонанс. Резонансные кривые.
  4. Дифференциальное уравнение затухающих колебаний и его решение. Основные характеристики затухающих колебаний. Логарифмический декремент затухания. Апериодический процесс.
  5. Рациональное управленческое решение. Способы принятия рационального решения. Списки. Дерево решений. Причинно-следственные диаграммы.
  6. Решение.
  7. Решение.
  8. Решение.
  9. Решение.
  10. Решение.
  11. Решение.
  12. Решение.

1а) Записываем расширенную матрицу системы:

.

2а) Выполняем прямой ход метода Гаусса.

.

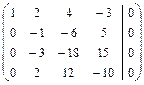
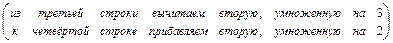
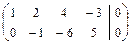Матрица системы приведена к трапециевидному виду с ненулевыми диагональными элементами. Соответствующая такой матрице система уравнений имеет бесконечно много решений, которые находим, выполняя обратный ход, и записываем в виде общего решения. Для записи общего решения указываем её базисные и свободные неизвестные. Базисный минор матрицы системы образуют столбцы коэффициентов при неизвестных и : 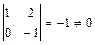. 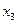Поэтому выбираем в качестве базисных – неизвестные и , тогда свободными будут неизвестные и .

3а) Выполняем обратный ход метода Гаусса.

Записываем систему уравнений, соответствующую последней расширенной матрице прямого хода: 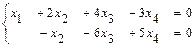. Свободным неизвестным придаём разные, произвольные постоянные значения: , , и последовательно из уравнений системы, начиная с последнего, находим значения всех базисных неизвестных: .

Тогда общее решение системы запишется в виде: .

4а) Выполняем проверку:

.

Ответ: .

б) .


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)