КОНТУР С ТОКОМ В МАГНИТНОМ ПОЛЕ

Рассмотрим действие магнитного поля на замкнутый контур с током. Для характеристики плоского контура с током вводят вектор магнитного момента , где S – площадь, ограниченная контуром, а направление нормали связано правилом правого винта с направлением тока в контуре (рис.84). Рассмотрим плоский контур в однородном магнитном поле. Сила, действующая со стороны магнитного поля на весь контур на основании закона Ампера равна: .

Так как сила тока и магнитная индукция при указанных условиях постоянны, то их можно вынести из-под знака суммы, а сумма элементарных векторов , в виде цепочки которых можно представить контур, равна нулю (рис.85).

Если результирующая сила равна нулю, то центр масс контура будет оставаться неподвижным, т. е. контур не будет двигаться поступательно, но возможно вращательное движение. Найдем вращающий момент сил, действующих на контур.

Рассмотрим простейший случай – линии вектора магнитной индукции лежат в плоскости контура. Разобьем контур на бесконечно узкие полоски шириной , параллельные линиям индукции.

Каждая полоска ограничена элементами тока, на которые со стороны магнитного поля действуют силы

и перпендикулярные плоскости чертежа и противоположные по направлению. , .

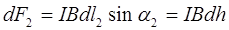Величина момента этой пары сил (равные по величине и противоположные по направлению):

Моменты сил действующих на все пары элементов тока контура направлены в одну строну и величина момента, действующего на весь контур .

Следовательно, в этом случае при , величина вращающего момента равна .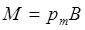

В общем случае и .

Вращающий момент равен нулю при и 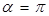. В первом случае и положение контура устойчивое.

Во втором случае и положение контура неустойчивое. На рис.86 представлено возникновение вращающего момента для прямоугольного контура с током.

Свободный контур в магнитном поле будет вращаться до устойчивого положения и, при достаточно малых размерах, может быть использован для исследования магнитного поля, а также определения вектора магнитной индукции: .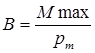

Магнитная индукция – векторная физическая величина, численно равная максимальному вращающему моменту, действующему со стороны магнитного поля на контур с единичным магнитным моментом в данной точке поля.

В устойчивом положении силы Ампера будут растягивать контур, а в неустойчивом положении эти силы будут вызывать сжатие контура (рис.87). В сильных магнитных полях возможна деформация замкнутых контуров, разрыв витков катушек.

РИС.87

Если контур с током не плоский, то каждый элемент контура можно представить в виде двух векторов, параллельных и перпендикулярных вектору индукции . Вращающий момент будет определяться «проекцией» контура на плоскость параллельную линиям индукции.

При повороте контура на малый угол совершается работа

, которая определяет изменение энергии контура при этом. Пусть контур жесткий (pm=const). Введем условие нормировки. При .

- энергия жесткого контура в магнитном поле при условии, что его энергия принята нулевой в положении, когда магнитный момент контура перпендикулярен вектору магнитной индукции.

Энергия контура минимальна, если магнитный момент параллелен вектору магнитной индукции, т. е. в этом случае контур находится в устойчивом положении равновесия. В неустойчивом положении

сложно. Поэтому рассмотрим случай, энергия контура будет максимальна.

В общем случае неоднородного поля описать поведение контура достаточно когда поле неоднородно, но величина магнитной индукции существенно изменяется в направлении линий магнитной индукции и практически не изменяется в перпендикулярных к ним направлениях (рис.88а).

РИС.88В этом случае также возникает момент сил, ориентирующий магнитный момент в направлении вектора магнитной индукции. В отличие от однородного поля результирующая сила, действующая на контур не равна нулю, так каждую силу можно представить в виде двух слагаемых

.

Сумма сил, лежащих в плоскости контура, определяет деформацию контура, а силы, перпендикулярные плоскости контура определяют втягивание контура в область более сильного поля (рис.88б).

Для элементарного контура (малых размеров) и в случае указанного неоднородного поля сила, действующая на него, может быть определена по следующей формуле

, т. е. для жесткого контура направление силы обусловлено изменением вектора магнитной индукции вдоль направления нормали к контуру.

Поиск по сайту: