Энергия электромагнитной волны. Вектор Пойтинга

Распространение электромагнитной волны сопровождается переносом энергии и импульса электромагнитного поля. Чтобы убедиться в этом, умножим скалярно первое уравнение Максвелла в дифференциальной форме на 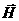, а третье – также скалярно на 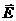, и вычтем полученные результаты один из другого. В результате будем иметь:

.

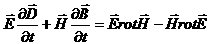Используя формулу векторного анализа , а также принимая во внимание материальные уравнения и , преобразуем написанное уравнение к виду:

или ,

где введены обозначения

;

.

Величина w – плотность энергии электромагнитного поля, переносимой волной: она слагается из плотности энергии электрического и магнитного полей. Вектор , имеющий смысл плотности потока энергии, носит название вектора Пойнтинга (Poynting J., 1852-1914).

Полученное уравнение выражает собой закон сохранения энергии для электромагнитного поля в дифференциальной форме. Оно показывает, что изменение энергии поля в выделенном объеме пространства за единицу времени происходит за счет потока вектора Пойнтинга через поверхность, охватывающую этот объем. Скорость переноса энергии называется групповой скоростью, она определяется как:

.

Отсюда следует размерность вектора Пойнтинга в СИ: .

Групповая и фазовая скорости волны связаны между собой соотношением де`Бройля (de Broglie L., 1892-1984):

.

В вакууме u= =c; в среде , поэтому в среде фазовая скорость электромагнитной волны может превышать скорость света в вакууме.

Наряду с энергией, электромагнитная волна переносит импульс поля. Плотность импульса 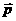электромагнитного поля связана с вектором Пойнтинга соотношением:

.

Из факта существования у электромагнитной волны импульса следует, что при ее падении на некоторую поверхность она будет оказывать давление на эту поверхность. Величина давления определяется по формуле:

,

где r – коэффициент отражения; - среднее значение плотности энергии волны.

Поиск по сайту: