АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Уравнения Максвелла в дифференциальной форме

Читайте также:
  1. V2: ДЕ 54 - Дифференциальные уравнения, допускающие понижение порядка
  2. V2: ДЕ 57 - Фундаментальная система решений линейного однородного дифференциального уравнения
  3. V2: Применения уравнения Шредингера
  4. V2: Уравнения Максвелла
  5. VI Дифференциальные уравнения
  6. А выходные характеристики системы являются зависимыми (эндогенными) переменными и в векторной форме имеют вид
  7. Алгебраические уравнения
  8. Анализ резисторной дифференциальной системы
  9. Анализ трансформаторной дифференциальной системы
  10. Аудит проведения международных расчетов в форме документарного аккредитива
  11. Аудит расчетов по форме безналичных расчетов
  12. Бесформенное предчувствие

Второе уравнение Максвелла в дифференциальной форме:

. (11.14)

Помимо уравнений (11.12) и (11.14) в систему уравнений Максвелла входит теорема Остроградского-Гаусса для электрического и магнитного полей:

, (11.15)

. (11.16)

Уравнение (11.16) выражает факт отсутствия свободных магнитных зарядов. Если ввести объемную плотность свободных зарядов r и учесть теорему Гаусса: , где dV – элемент объема V, можно получить третье и четвертое уравнения Максвелла в дифференциальной форме:

, (11.17)

. (11.18)

Полная система уравнений Максвелла: , ,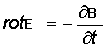

,

дополняется материальными уравнениями, связывающими векторы E, D, H и B с величинами, описывающими электрические и магнитные свойства среды:

, , . (11.19)

При заданных начальных условиях система уравнений Максвелла имеет единственное решение.

Теория Максвелла не только объяснила уже известные факты, но и предсказала новые явления. Максвелл теоретически предсказал существование электромагнитных волн, распространяющихся в пространстве с конечной скоростью, что в дальнейшем получило блестяще подтверждение.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)