 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Частица в глубокой одномерной потенциальной яме. Квантование энергии
Найдем собственные значения энергии и соответствующие им собственные функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме. Предположим что, частица можетдвигаться только вдоль оси x. Пусть движение ограничено непроницаемыми для частицы стенками x = 0, 
и x =?. Потенциальная энергия U имеет вид:
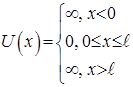
Уравнение Шредингера для стационарных состояний для одномерной задачи 
За пределы потенциальной ямы частица попасть не сможет, поэтому вероятность обнаружения частицы вне ямы равна 0.Следовательно, и Ψ за пределами ямы равна 0.Из условий непрерывности следует, что Ψ = 0 и на границах ямы т.е.Ψ(0) = Ψ(?) = 0 В пределах ямы (0 £ x £ l) U = 0 и уравнение Шредингера.
введя 
получим 
Общее решение 
;
из граничных условий следуетy(0) = 0,
Таким образом В = 0. Следовательно, 
Из граничного условия 
Следует 
Þ 
Тогда 
Энергия Еn частицы в "потенциальной яме" с бесконечно высокими стенками принимает лишь определенные дискретные значения, т.е. квантуется. Квантованные значения энергии Еn называются уровнями энергии, а число n, определяющее энергические уровни частицы, называется главным квантовымчислом. Т.е. частицы в "потенциальной яме" могут находиться только на определенном энергетическом уровне Еn (или находятся в квантовом состоянии n)Собственные функции: 
А найдем из усилия нормировки
- плотность вероятности. Из рис. видно, что плотность вероятности меняется в зависимости от n: при n = 1 частица, скорее всего, будет посередине ямы, но не на краях, при n = 2 - будет или в левой или в правой половине, но не посередине ямы и не на краях, и т.д. Т.е нельзя говорить о траектории движения частицы.
Энергетический интервал между соседними уровнями энергии: 
При n = 1 имеет наименьшую энергию отличную от нуля 
Наличие минимума энергии следует из соотношения неопределенностей, т.к. 
,
C ростом n расстояние между уровнями уменьшается и при n ® ¥ Еn практически непрерывны, т.е. дискретность сглаживается, т.е. выполняется принцип соответствия Бора: при больших значениях квантовых чисел законы квантовой механики переходят в законы классической физики.
Общая трактовка принципа соответствия: всякая новая, более общая теория является развитием классической, не отвергает ее полностью, а включает в себя классическую, указывая границы её применимости.
Поиск по сайту: