АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

ТЕОРЕМА СУЩЕСТВОВАНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

Читайте также:
  1. I. Правила поведения в условиях вынужденного автономного существования.
  2. S-M-N-теорема, приклади її використання
  3. V2: ДЕ 39 - Интегральное исчисление функции одной переменной. Приложения определенного интеграла
  4. А) Формы существования
  5. Аддитивность интеграла Римана.
  6. Билет 3. Назовите основные условия существования политической деятельности
  7. Биологическая форма материи: единство, сущность, способ существования, направленность эволюции.
  8. Биосфера и закономерности ее существования
  9. В заданиях 1-8 вычислить значение определенного интеграла.
  10. Внешние эффекты (экстерналии). Теорема Коуза.
  11. Внешние эффекты трансакционные издержки. Теорема Коуза
  12. Внешние эффекты, их виды и последствия. Теорема Коуза

Если функция f(x) непрерывна на отрезке [ a, в ], то предел интегральной суммы существует и не зависит ни от способов разбиения на отрезке [ a, в ] на элементарные отрезки, ни от выборов точек на этих отрезках.

Если функция f(x) на отрезке [ a, в ] положительна, то определенный интеграл 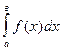геометрически представляет собой площадь криволинейной трапеции - фигуры, ограниченной линиями

 

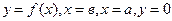
ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

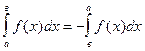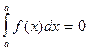1. ; 2. ; 3. ;

4. ;

4.

 

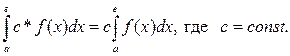
ФОРМУЛА НЬЮТОНА - ЛЕЙБНИЦА

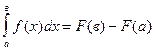, где F(x) - первообразная функции f(x), т.е. F¢(x) = f(x).

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)