АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 1-ГО ПОРЯДКА

Читайте также:
  1. II ОБЩИЕ НАЧАЛА ПУБЛИЧНО-ПРАВОВОГО ПОРЯДКА
  2. II. САКРАЛЬНАЯ ГЕОМЕТРИЯ: МЕТАФОРА УНИВЕРСАЛЬНОГО ПОРЯДКА
  3. IV.1. Общие начала частной правозащиты и судебного порядка
  4. V2: ДЕ 53 - Способы решения обыкновенных дифференциальных уравнений первого порядка
  5. V2: ДЕ 54 - Дифференциальные уравнения, допускающие понижение порядка
  6. V2: ДЕ 57 - Фундаментальная система решений линейного однородного дифференциального уравнения
  7. V2: ДЕ 6 - Линейные отображения. Определители второго порядка
  8. V2: Применения уравнения Шредингера
  9. V2: Уравнения Максвелла
  10. VI Дифференциальные уравнения
  11. Адаптивная полиномиальная модель первого порядка
  12. Алгебраические уравнения

Дифференциальными уравнениями (д. у.) 1-го порядка называются уравнение вида F(x, у, у¢) = 0 (1)

или у¢ = f(x, у), что можно записать и так (1¢)

dу = f(x,у)dx. (1¢¢)

Обозначим через Д область существования решения (1) - (1¢¢).

Общим решением д.у. (1) - (1¢¢) называется функция у = , (2)

где С - произвольная константа, удовлетворяющая условиям:

а) она является решением д.у. при любом С;

б) при любых начальных условиях . (*)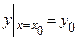

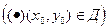, найдется такое значение С = С0, что функция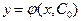

удовлетворяет условиям (*).

Нахождение такого С = С0 по условиям (*) называется решением задачи Коши. Найденная таким образом функция 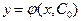называется иначе частным решением д.у.

Если решение д.у. найдено в виде Ф(х, у, С) =0, оно называется общим интегралом этого уравнения.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)