АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

ЗАДАЧА № 2. 1. Характеристическое уравнение:

Читайте также:
  1. VI. Общая задача чистого разума
  2. В задачах 13.1-13.20 даны выборки из некоторых генеральных совокупностей. Требуется для рассматриваемого признака
  3. ВАША ЗАДАЧА
  4. Вопрос 2 Проверка и оценка в задачах со случайными процессами на примере решения задач экозащиты, безопасности и риска.
  5. Вот дела не задача
  6. Глава 10 Системный подход к задачам управления. Управленческие решения
  7. ГЛАВА 2.1. ЗАЩИТА ИННОВАЦИЙ КАК ЗАДАЧА УПРАВЛЕНИЯ ИННОВАЦИОННЫМИ ПРОЦЕССАМИ
  8. Глава 4. Математические основы оптимального управления в экономических задачах массового обслуживания
  9. Двойственная задача линейного программирования.
  10. Доклад о задачах власти Советов
  11. Доклад об экономическом положении рабочих Петрограда и задачах рабочего класса на заседании рабочей секции Петроградского совета рабочих и солдатских депутатов
  12. Задание 48: (Кейс 2 подзадача 1)

1. у¢¢ - 4а112 у¢ + 3а111у = 0; 2. у¢¢ + 2а22 у¢ + а222у = 0;

3. у¢¢ + а21у¢ = 0; 4. у¢¢ + а332у = 0.

1. Характеристическое уравнение: .

Легко находим, что к1 = 3а11, к2 = а11 (корни вещественные, различные). Это 1-й случай табл. 1. Тогда - общее решение.

2. Характеристическое уравнение: .

Далее применить табл. 1 и самостоятельно записать уо.о..

3. Характеристическое уравнение: .

Закончить пример самостоятельно.

4. Характеристическое уравнение: .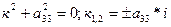

Закончить пример самостоятельно.

В следующих примерах найти частные решения д. у. (уч.о.), удовлетворяющие заданным начальным условиям.

5. у¢¢ - 3а12 у¢ + 2а12у = 0, у(1) = в1, у¢(1) = в2;

6. у¢¢ - а222у = 0, у(0) = в2, у¢(0) = в3.

5. Характеристическое уравнение:

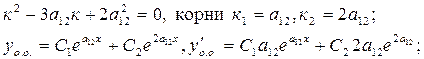
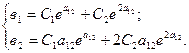
Решить систему, найти С1, С2 и уч .о..

6. Характеристическое уравнение:

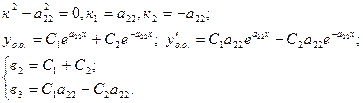
Решить систему, найти С1, С2 и уч.о..
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)