ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ

Выше было показано, что из неправильной рациональной дроби можно выделить целую часть и представить эту дробь как сумму целой ее части и правильной дроби. Поэтому будем рассматривать только интегрирование правильных дробей.

Всякую правильную рациональную дробь нужно представить в виде суммы простейших, которые имеют вид:

1. , 2. , 3. ,

где А, В, а, в, р, q - действительные числа.

Теперь нужно научиться всякую правильную рациональную дробь представить как сумму простейших. Для этого вначале разложим знаменатель этой дроби на произведение множителей типа (х - а) и (х² + рх + q), причем квадратный трехчлен х² + рх + q имеет дискриминант Д < 0. Если Д > 0, то такой квадратный трехчлен можно разложить на линейные множители:

x² + px + q = (x - x₁)(x - x₂), где х₁ и х₂ - корни данного трехчлена.

Будем руководствоваться следующими приемами:

1. Каждому линейному множителю вида (х - а) соответствует дробь , где А -

неизвестный пока коэффициент;

2. Каждому множителю (х - в)^к соответствует сумма из К простых дробей

;

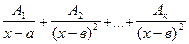3. Каждому множителю х² + рх + q (Д < 0) соответствует дробь вида .

Поиск по сайту: