АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА ВРАЩЕНИЯ

Читайте также:
  1. Аллотропические превращения железа при нагреве и охлаждении. Гистерезис.
  2. Анализ общего объема и ассортиментной структуры розничного товарооборота
  3. Анализ объема и структуры выпуска продукции
  4. Анализ объема продаж предприятий оптовой торговли
  5. Анализ резервов роста объема производства
  6. Анализ резервов роста объема производства
  7. Анализ факторов изменения объема реализации продукции
  8. Анализ функциональной связи между затратами, объемом продаж и прибылью. Определение безубыточного объема продаж и зоны безопасности предприятия
  9. Анализ чувствительности прибыли к изменению затрат, цены и объема продаж
  10. Б) Вычисление тригонометрических функций.
  11. Билет 17(Цена спроса. Цена предложения. Равновесная цена. Механизм возвращения к равновесной цене. Функции цен в рыночной экономике.)
  12. Брожение. Пути превращения глюкозы в ПВК. Общая характеристика процессов брожения

Рассмотрим криволинейную трапецию, ограниченную кривой y = f(x) и прямыми у = 0, х = в. Пусть эта трапеция вращается вокруг оси Ох. Тогда объем тела вращения вычисляется по формуле .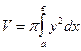

Если фигура, ограниченная кривыми y = f1(x); y = f2(x) (0 ≤ f1(x) ≤ f2(x)) и прямыми х = а, х = в, вращается вокруг оси Ох, то объем тела вращения .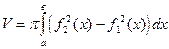

Рассмотрим криволинейную трапецию х = j(у), х = 0, у = 1, у = d. Объем тела вращения, полученного путем вращения этой трапеции вокруг оси Оу, .

 

ЗАДАЧА № 12

Найти объем тела вращения

       
 
   
Х
 

 


 

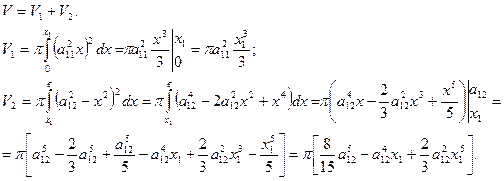
2. .

х

 

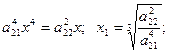
ДВОЙНОЙ ИНТЕГРАЛ


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)