Метод экспертной оценки ранжированием

При экспертном оценивании качества аналогичных, но не идентичных объектов методом ранжирования, эксперты представляют объекты в виде (возрастающего) ранжированного ряда. Численное определение итоговых оценок качества осуществляют поэтапно.

При этом:

1) Все объекты оценивания Q_i нумеруются произвольно.

2) Эксперты ранжируют объекты по шкале порядка.

3) Ранжированные ряды объектов, составленные экспертами, сопоставляются.

Например:

Эксперт № 1 – Q ₅ < Q ₃ < Q ₂ < Q ₁ < Q ₆ < Q ₄ < Q ₇

Эксперт № 2 – Q ₅ < Q ₃ < Q ₂ < Q ₆ < Q ₁ < Q ₄ < Q ₇

Эксперт № 3 – Q ₅ < Q ₂ < Q ₃ < Q ₁ < Q ₆ < Q ₇ < Q ₄

Ранги R: 1 2 3 4 5 6 7

Наименее значимому объекту (предмету или его свойству), поставленному экспертом на первое место в возрастающем ранжированном ряду объектов, присваивается 1 ранг (R =1), следующему 2 ранга (R =2) и т.д. Наибольшее число рангов R равно числу оцениваемых объектов. В нашем примере число объектов m =7 и R _max=7. Число рангов объекта соответствует его месту в ранжированном ряду.

4) Определяем суммы рангов каждого объекта полученных от всех n экспертов.

В данном примере это:

,

,

,

,

,

,

.

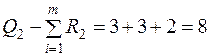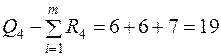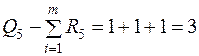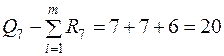5) На основании полученных сумм рангов строят обобщенный ранжированный ряд.

В нашем примере: Q ₅ < Q ₃ < Q ₂ < Q ₁ < Q ₆ < Q ₄ < Q ₇.

6) Рассчитывают обобщенные экспертные оценки качества рассматриваемых объектов (коэффициенты весомости)

. (31)

где n – количество экспертов; m – число оцениваемых объектов или показателей; R_ij – ранг j -го показателя свойства, который дал i -й эксперт.

Общее количество рангов в данном примере

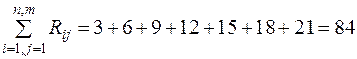
В примере:

g ₁ = 13 / 84 = 0,15; g ₂ = 8 / 84 = 0,10; g ₃ = 7 / 84 = 0,08;

g ₄ = 19 / 84 = 0,23; g ₅ = 3 / 84 = 0,04; g ₆ = 14 / 84 = 0,17;

g ₇ = 20 / 84 = 0,24.

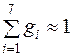
Анализируя полученные результаты, можно указать какой объект лучше и на сколько.

7) Точность экспертных оценок определяют по согласованности мнений экспертов.

Степень совпадения оценок экспертов характеризует качество экспертизы и выражается коэффициентом конкордации W (0< W <1):

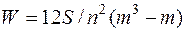, (32)

где S – сумма квадратов отклонений рангов или баллов каждого объекта от среднего арифметического значения;

n – количество экспертов;

m – количество оцениваемых объектов.

Значение S рассчитывают по формуле:

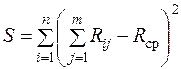(33)

или

,

где ;

R_ij – оценка в рангах данная i -му объекту j -м экспертом;

R _cp – среднеарифметическое значение рангов.

При W =0 имеем абсолютную несогласованность, а при W =1,0 – полное совпадение мнений.

В примере:

R _cp = (13 + 8 + 7 + 19 + 3 + 14 + 20) / 7 = 84 / 7 = 12

S = 1² + 4² + 5² + 7² + 9² + 2² + 8² = 240

W = 12 ´ 240 / (9 ´ (343 – 7)) = 2880 / 3024 = 0,87

Повысить точность экспертных оценок показателей качества можно, если произвести двукратное сопоставление и ранжирование.

Поиск по сайту: