АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Основные свойства определителей

Читайте также:
  1. B. Основные принципы исследования истории этических учений
  2. F. Метод, основанный на использовании свойства монотонности показательной функции .
  3. I. Значение и задачи учета. Основные документы от реализации продукции, работ, услуг.
  4. I. ОСНОВНЫЕ ПОНЯТИЯ (ТЕРМИНЫ) ЭКОЛОГИИ. ЕЕ СИСТЕМНОСТЬ
  5. I. Основные сведения
  6. I. ОСНОВНЫЕ СПОСОБЫ ПЕРЕДВИЖЕНИЯ И ПРЕОДОЛЕНИЯ ПРЕПЯТСТВИЙ
  7. I. ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
  8. I. Основные термины и предпосылки
  9. I. ОСНОВНЫЕ ТРЕБОВАНИЯ К СИСТЕМАМ ЭЛЕКТРОСНАБЖЕНИЯ
  10. I. Размеры и тинкториальные свойства волокон
  11. I.3. Основные этапы исторического развития римского права
  12. II Съезд Советов, его основные решения. Первые шаги новой государственной власти в России (октябрь 1917 - первая половина 1918 гг.)

1. «Равноправность строк и столбцов». Определитель матрицы не изменится, если его строки заменить столбцами, и наоборот (т.е. транспонировать)

2. При перестановке двух строк (или столбцов) определитель изменит свой знак на противоположный:

3. Определитель с двумя одинаковыми строками или столбцами равен нулю.

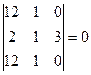
4. Общий множитель всех элементов строки (или столбца) можно вывести за знак определителя:

5. Если все элементы двух строк (столбцов) определителя пропорциональны, то определитель равен нулю.

6. Если к какой-либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, то определитель не изменит своей величины:

7. Если элементы какой-либо строки (столбца) определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей:

8. Треугольный определитель, у которого все элементы, лежащие выше (или ниже) главной диагонали, - нули, равен произведению элементов главной диагонали:


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)