Миноры и алгебраические дополнения элементов определителя

Минором 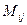некоторого элемента 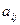определителя n-го порядка называется определитель n-1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент.

Например, Минор М₁₂ , соответствующий элементу определителя

,

получается, если вычеркнуть из определителя D первую строку и второй столбец, т.е.

.

Пример 3. Записать все миноры определителя

Решение.

=-57, =42, =63,

=-21, =24, =9,

=-15, =-6, =-9.

Алгебраическим дополнением элемента 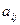определителя называется минор 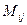этого элемента, взятый со знаком . Алгебраическое дополнение элемента 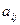принято обозначать .

Таким образом, .

Знаки алгебраического дополнения А_ij:

Пример 4. Найти алгебраические дополнения элементов определителя

Решение.

Теорема. «О разложении определителя по элементам строки или столбца». Сумма произведений элементов любой строки (или столбца) определителя D на их алгебраические дополнения равна этому определителю, т.е.

или .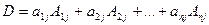

Эти соотношения называются разложением определителя по элементам i-ой строки или j-го столбца.

Для разложения определителя обычно выбирают тот ряд, где есть нулевые элементы, т.к. соответствующие им слагаемые в разложении будут равны нулю.

Пример 5. Определитель разложить:

1. по элементам второй строки;

2. по элементам первого столбца.

Решение.

1.

2.

Если определитель имеет четвертый или более высокий порядок, то его также можно разложить по элементам строки или столбца.

Пример 6. Вычислить определитель матрицы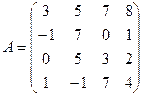

Решение. Разложим определитель по элементам 1-го столбца.

Перечислим различные способы вычисления определителей.

1. Определитель можно вычислить, используя непосредственно его определение. Этим способом удобно находить определители 2-го и 3-го порядков (треугольник Саррюса), а для определителя более высокого порядка применим следующий способ.

2. Определитель можно вычислить с помощью его разложения по элементам строки или столбца.

3. Определитель можно вычислить способом приведения к треугольному виду. Этот способ основан на том, что в силу свойства 8 треугольный определитель равен произведению элементов главной диагонали.

Чтобы получить треугольный определитель, нужно используя свойство 6, к какой-либо строке (или столбцу) заданного определителя прибавлять соответствующие элементы другой стоки (или столбца), умноженные на одно и тоже число, до тех пор пока не придем к определителю треугольного вида.

Контрольные вопросы

1. Что называется определителем матрицы?

2. Как вычислить определитель третьего порядка по схеме треугольников?

3. Что называется минором?

4. Что называется алгебраическим дополнением элемента определителя?

5. Как разложить определитель по элементам столбца или строки?

6. Какие способы вычисления определителя вам известны?

7. Перечислите свойства определителей.