 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Тема: Решение системы линейных уравнений
Цели занятия:
К занятию надо знать.
Ø Формулировку теоремы Крамера.
Ø Формулы Крамера.
Ø В каком случае система линейных уравнений не имеет решения или имеет бесчисленное множество решения.
Ø Правило решения матричного уравнения.
Ø Процесс решения систем линейных уравнений по методу Гаусса.
На занятии надо научиться:
Ø Решать систему линейных уравнений формулами Крамера.
Ø Решать систему линейных уравнений матричным методом.
Ø Решать систему линейных уравнений методом Гаусса.
Порядок работы на занятии:
1. Повторить формулы Крамера.
2. Повторить правило решения матричного уравнения.
3. Повторить процесс решения систем линейных уравнений по методу Гаусса.
4. Рассмотреть образец решения задания 1.
5. Выполнить задание 2.
6. Выполненное задание покажите преподавателю. Возможен устный
Задание 1. Решить систему уравнений: 
Ø Формулами Крамера
Ø Матричным методом
Ø Методом Гаусса
Решение.
Ø Формулами Крамера:
D = 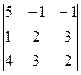 = 20 – 12 – 3+8 – 45+2= – 30;
= 20 – 12 – 3+8 – 45+2= – 30;
Dx = 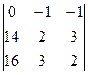 = 0 – 48 – 42 +32 + 28 – 0 = – 30;
= 0 – 48 – 42 +32 + 28 – 0 = – 30;
Dy = 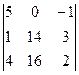 = 140 + 0 – 16 + 56 – 0 – 240 = – 60;
= 140 + 0 – 16 + 56 – 0 – 240 = – 60;
Dz = 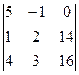 = 160 – 56 + 0 – 0+16 –210 = – 90;
= 160 – 56 + 0 – 0+16 –210 = – 90;
x = Dx/D = 1; y = Dy/D = 2; z = Dz/D = 3.
Ответ: (1,2,3)
Ø Матричным методом:
Х = 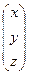 , B =
, B = 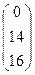 , A =
, A = 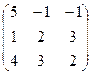
Найдем обратную матрицу А-1.
D = det A = 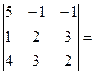 20 – 12 – 3 + 8 – 45+2= -30.
20 – 12 – 3 + 8 – 45+2= -30.
А11 = 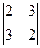 = -5; А21 =
= -5; А21 = 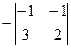 = -1; А31 =
= -1; А31 = 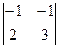 = -1;
= -1;
А12 = 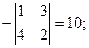 А22 =
А22 = 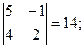 А32 =
А32 = 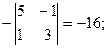
А13 = 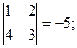 А23 =
А23 = 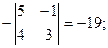 А33 =
А33 = 
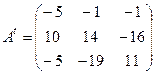 A-1 =
A-1 =  ;
;
Находим матрицу Х.
Х = 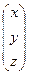 = А-1В =
= А-1В = 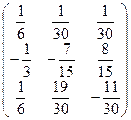 ×
× 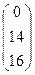 =
= 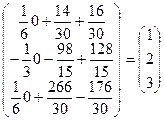 .
.
Итого решения системы: x =1; y = 2; z = 3
Ø Методом Гаусса
Составим расширенную матрицу системы.


Таким образом, исходная система может быть представлена в виде:
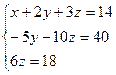 , откуда получаем: z = 3; y = 2; x = 1.
, откуда получаем: z = 3; y = 2; x = 1.
Задание 2. Решить систему тремя способами:
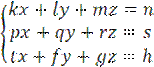
Ø по формулам Крамера
Ø матричным методом;
Ø методом Гаусса.
Соответствующие коэффициенты выберите из таблицы:
| Вариант | k | l | m | n | p | q | r | s | t | f | g | h |
| -1 | -2 | |||||||||||
| -1 | -4 | -1 | -1 | |||||||||
| -2 | ||||||||||||
| -1 | -2 | -2 | ||||||||||
| -1 | ||||||||||||
| -3 | -2 | |||||||||||
| -1 | -1 | |||||||||||
| -1 | -7 | -2 | ||||||||||
| -1 | -1 | |||||||||||
| -1 | -1 |
Занятие 8. (Контрольная работа)
Поиск по сайту: