АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Тема: Решение систем линейных уравнений

Читайте также:
  1. A) к любой экономической системе
  2. A) прогрессивная система налогообложения.
  3. c) Определение массы тела по зависимости момента инерции системы, совершающей крутильные колебания от квадрата расстояния тела до оси вращения
  4. C) Систематическими
  5. CASE-технология создания информационных систем
  6. ERP и CRM система OpenERP
  7. HMI/SCADA – создание графического интерфейса в SCADА-системе Trace Mode 6 (часть 1).
  8. I Понятие об информационных системах
  9. I СИСТЕМА, ИСТОЧНИКИ, ИСТОРИЧЕСКАЯ ТРАДИЦИЯ РИМСКОГО ПРАВА
  10. I. Компоненты систем
  11. I. Основні риси політичної системи України
  12. I. ОСНОВНЫЕ ПОНЯТИЯ (ТЕРМИНЫ) ЭКОЛОГИИ. ЕЕ СИСТЕМНОСТЬ
  Вариант 1 Решить систему тремя способами: - по формулам Крамера - матричным методом; - методом Гаусса.   Вариант 2 Решить систему тремя способами: - по формулам Крамера - матричным методом; - методом Гаусса.
Ответ: (-1,-3,4)   Вариант 3 Решить систему тремя способами: - по формулам Крамера; - матричным методом; - методом Гаусса. Ответ: (-1,0,1)   Вариант 4 Решить систему тремя способами: - по формулам Крамера; - матричным методом; - методом Гаусса.
  Вариант 5 Решить систему тремя способами: - по формулам Крамера; - матричным методом; - методом Гаусса.     Вариант 6 Решить систему тремя способами: - по формулам Крамера; - матричным методом; - методом Гаусса.  
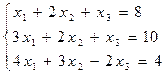
Вариант 7 Решить систему тремя способами: - по формулам Крамера - матричным методом; - методом Гаусса. Вариант 8 Решить систему тремя способами: - по формулам Крамера; - матричным методом; - методом Гаусса.  
    Вариант 9 Решить систему тремя способами: - по формулам Крамера; - матричным методом; - методом Гаусса.     Вариант 10 Решить систему тремя способами: - по формулам Крамера; - матричным методом; - методом Гаусса.  
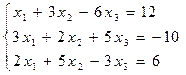
Вариант 11 Решить систему тремя способами: - по формулам Крамера; - матричным методом; - методом Гаусса. Вариант 12 Решить систему тремя способами: - по формулам Крамера; - матричным методом; - методом Гаусса.  
Вариант 13 Решить систему тремя способами: - по формулам Крамера; - матричным методом; - методом Гаусса. Вариант 14 Решить систему тремя способами: - по формулам Крамера; - матричным методом; - методом Гаусса.
Вариант 15 Решить систему тремя способами: - по формулам Крамера; - матричным методом; - методом Гаусса.   Вариант 16 Решить систему тремя способами: - по формулам Крамера; - матричным методом; - методом Гаусса.
Вариант 17 Решить систему тремя способами: - по формулам Крамера - матричным методом; - методом Гаусса.   Вариант 18 Решить систему тремя способами: - по формулам Крамера - матричным методом; - методом Гаусса.  
Вариант 19 Решить систему тремя способами: - по формулам Крамера - матричным методом; - методом Гаусса. Вариант 20 Решить систему тремя способами: - по формулам Крамера - матричным методом; - методом Гаусса.  
Вариант 21 Решить систему тремя способами: - по формулам Крамера - матричным методом; - методом Гаусса. Вариант 22 Решить систему тремя способами: - по формулам Крамера - матричным методом; - методом Гаусса.

Литература

1. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы. Учебн. Пособие. – М.: Наука, 1990.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2–х ч.: Учеб.пособие для втузов. – 5–е изд., испр. – М.: Высш.шк., 1999. – 304 с.: ил.
3. Шипачев В.С. Высшая математика. Учеб.для вузов.-М.: Высш.школа. 1998.- 497с.: ил.
4. Шипачев В.С. Задачник по высшей математике. Учеб.пособие для вузов.-М.: Высш.школа. 1998.- 304с.: ил.
5. В. Т. Лисичкин, И. Л. Соловейчик. Математика. Учеб.пособие для техникумов.-М.: Высш.школа. 1991. – 480 с.: ил
6. Дмитрий Письменный Конспект лекций по высшей математике Учеб.пособие для втузов. – 3-е изд.. – М.: Айрис – пресс; 2005. – 608 с.: ил.
7. Н. В. Богомолов Практические занятия по математике: Учеб.пособие для втузов. – 4–е изд., стер. – М.: Высш.шк.,1997. – 495с. 8. В. Д. Черненко ВЫСШАЯ МАТЕМАТИКА В примерах и задачах 1 том Учебное пособие для вузов. В 3 т.: Т. 1.— СПб.: Политехника, 2003.— 703 с: ил. 9. Математика. Контрольные задания / Сост.: В.И. Фомин. Тамбов: Изд-во Тамб. гос. техн. ун-та, 2004. 88 с. 10. Учебно-методический комплекс дисциплины «Математика». Раздел 1 «Линейная и векторная алгебра». Контрольно-измерительные материалы. – Уфа: Издательство УГНТУ, 2007. – 175 с

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)