Тема: Системы линейных уравнений

План:

1. Основные понятия.

2. Решение невырожденных линейных системформулами Крамера.

Основные понятия.

Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида

(1)

где числа a₁₁, a₁₂,…, a_mn, называются коэффициентами системы или коэффициентами при неизвестных.

Первый индекс у коэффициентов системы указывает на номер уравнения, второй на номер неизвестного, при котором записан этот коэффициент.

Числа b₁, b₂,…, b_m называются свободными членами. Система линейных уравнений называется однородной, если все свободные члены равны нулю, если же, хотя бы одно из них отлично от нуля, то неоднородной.

Решением системы (1) называется любая совокупность чисел x₁, x₂, x₃,…,x_n - подстановка которой в (1) обращает каждое уравнение этой системы в верное числовое равенство. Система, имеющая хотя бы одно решение, называется совместной, имеющая только одно решение определенной, имеющая более одного решения - неопределенной, не имеющая ни одного решения - несовместной.

Решить систему (1) - это значит указать все множество ее решений или доказать ее несовместность.

Систему (1) удобно записать в компактной матричной форме А∙Х=В. Здесь А – матрица коэффициентов системы, называемая основной матрицей:

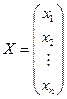- вектор-столбец из неизвестных , - вектор-столбец из свободных членов .

Произведение матриц А∙Х определено, так как в матрице А столбцов столько же, сколько строк в матрице Х (n штук).

Расширенной матрицей системы называется матрица системы, дополненная столбцом свободных членов

2. Решение линейных системформулами Крамера.

Пусть дана система n линейных уравнений с n неизвестными

или в матричной форме А∙Х=В. Основная матрица такой системы квадратная.

Определитель этой матрицы называется определителем системы. Если определитель системы отличен от нуля, то система называется невырожденной.

Теорема Крамера. Система n уравнений с n неизвестными, определитель которой отличен от нуля, всегда имеет решение и притом единственное, и это решение находится по формулам:

, , , …,

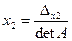где D_хi – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов b_i.

Оно находится следующим образом: значение каждого из неизвестных равно дроби, знаменателем которой является определитель системы, а числитель получается из определителя системы замены столбца коэффициентов при искомом неизвестном на столбец свободных членов.

Пусть 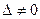. Если в определителе системы заменить поочередно столбцы коэффициентов при на столбец свободных членов, то получим n определителей (для n неизвестных)

, , …,

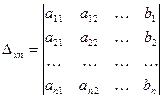
Тогда формулы Крамера для решения системы n линейных уравнений с n неизвестными запишутся так: 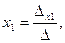…, или короче где i=1, 2, …, n.

Рассмотрим случай, когда определитель системы равен нулю. Здесь возможны два варианта:

1. 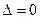и каждый определитель . Это имеет место только тогда. Когда коэффициенты при неизвестных 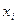пропорциональны, т.е. каждое уравнение системы получается из первого уравнения умножением обеих его частей на число k. Очевидно что при этом система имеет бесчисленное множество решений.

2. 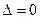и хотя бы один из определителей . Это имеет место только тогда, когда коэффициенты при неизвестных, кроме 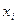, пропорциональны. При этом получается система из противоречивых уравнений, которая не имеет решений.

Пример 1. Решить систему двух линейных уравнений с двумя неизвестными

Решение. Вычислим определитель системы и определители и :

.

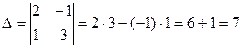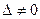
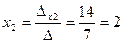
Ответ: x₁=1, x₂=2

Поиск по сайту: