 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Операция умножения матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы
Произведением матрицы  на матрицу
на матрицу  называется матрица
называется матрица  такая, что
такая, что  , где
, где 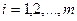 ,
,  .
.
Получение элемента  схематично изображается так:
схематично изображается так:




j
Вообще, чтобы получить элемент, стоящий на пересечении i-ой строки и j-го столбца матрицы произведения, нужно все элементы i-ой строки ( ,
, 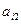 , …,
, …,  ) матрицы А умножить на соответствующие элементы j-го столбца (
) матрицы А умножить на соответствующие элементы j-го столбца (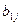 ,
,  , …,
, …,  ) матрицы В и полученные произведения сложить.
) матрицы В и полученные произведения сложить.
Если матрицы А и В произвольного размера, то произведения АВ и ВА не всегда существуют.
Рассмотрим умножение квадратных матриц второго порядка.
Пусть  .
.
Произведением этих матриц называется матрица 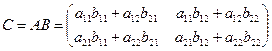
чтобы найти элемент 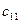 первой строки и первого столбца матрицы С, нужно каждый элемент первой строки матрицы А (т.е.
первой строки и первого столбца матрицы С, нужно каждый элемент первой строки матрицы А (т.е.  и
и  ) умножить на соответствующий элемент первого столбца матрицы В (т.е.
) умножить на соответствующий элемент первого столбца матрицы В (т.е. 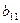 и
и  ) и полученные произведения сложить
) и полученные произведения сложить  ;
;
чтобы получить элемент 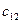 первой строки и второго столбца матрицы С, нужно умножить все элементы первой строки (
первой строки и второго столбца матрицы С, нужно умножить все элементы первой строки ( и
и  ) на соответствующие элементы второго столбца (т.е.
) на соответствующие элементы второго столбца (т.е.  и
и  ) и полученные произведения сложить:
) и полученные произведения сложить: 
аналогично находится элементы  и
и  .
.
Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко доказать, что А∙Е=Е∙А=А, где А-квадратная матрица, Е- единичная матрица того же размера.
Пример 3. Найти произведение матриц А и В, если
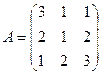 ,
, 
Решение. Так как матрица  и матрица
и матрица 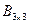 , то матрица произведения
, то матрица произведения  и содержит 9 элементов. Найдем каждый элемент матрицы-произведения:
и содержит 9 элементов. Найдем каждый элемент матрицы-произведения:
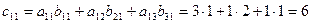


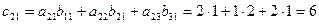


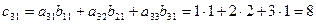

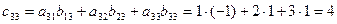

Пример 3. Найти произведение матриц А и В, если
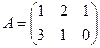

Решение. Произведение матриц А∙В не определенно, так как число столбцов матрицы А (3) не совпадает с числом строк матрицы В (2). При этом определенно произведение В∙А. Так как матрица  и матрица
и матрица  , то матрица произведения
, то матрица произведения  и содержит 6 элементов.
и содержит 6 элементов.
В∙А= 
Умножение матриц обладают следующими свойствами:
1. А∙(В∙С)= (А∙В)∙С;
2. А∙(В+С)=АВ+АС;
3. (А+В)∙С=АС+ВС;
4. α(АВ)=(αА)В.
5. 
Контрольные вопросы
1. Что называется матрицей?
2. Что называется матрицей – строкой? Матрицей – столбцом?
3. Какие матрицы называются прямоугольными? Квадратными?
4. Какие матрицы называются равными?
5. Что называется главной диагональю матрицы?
6. Какая матрица называется диагональной?
7. Какая матрица называется единичной?
8. Какая матрица называется треугольной?
9. Что значит «Транспонировать» матрицу?
10. Что называется суммой матриц?
11. Что называется произведением матрицы на число?
12. Как найти произведение двух матриц?
13. В чем состоит обязательное условие существование произведения матриц?
14. Какими свойствами обладает произведение матриц
Занятие 2. (практическое)
Поиск по сайту: