Обратная матрица. Пусть А – квадратная матрица n-го порядка

Пусть А – квадратная матрица n-го порядка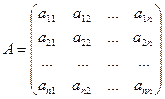

Квадратная матрица А^-1 порядка n называется обратной матрицей для данной матрицы A, если 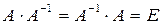, где − E единичная матрица.

Квадратная матрица А называется вырожденной, если ее определитель detA

равен 0 т.е. detA=0. В противном случае (detA≠0) матрица А называется невырожденной.

Обратная матрица 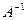имеет те же размеры, что и матрица А.

Теорема. Всякая невырожденная матрица А имеет обратную матрицу A^-1, определяемую формулой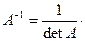

где A₁₁, A₁₂, …, A_nn есть алгебраические дополнения соответствующих элементов a₁₁, a₁₂,…, a_nn матрицы А.

Правило вычисления обратных матриц n-го порядка

1. Находят определитель матрицы А т.е. detA.

2. Находят алгебраические дополнения всех элементов 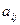матрицы А.

3. Умножают полученную транспонированную матрицу на .

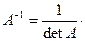
Нахождение обратной матрицы имеет большое значения при решении систем линейных уравнений и в вычислительных методах линейного программирования.

Поиск по сайту: