Решение систем линейных уравнений матричным методом. Пусть дана система уравнений

Пусть дана система уравнений

Рассмотрим матрицу, составленную из коэффициентов при неизвестных .

Свободные члены и неизвестные можно записать в виде матриц-столбцов: ,

Тогда используя правило умножения матриц, эту систему уравнений можно записать так:

= или АХ=В

Это равенство называется простейшим матричным уравнением.

Чтобы решить матричное уравнение, нужно:

1. Найти обратную матрицу .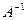

2. Найти произведение обратной матрицы 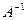на матрицу – столбец свободных членов В, т.е. .

3. Пользуясь определением равных матриц, записать ответ.

Пример 2. Решить систему уравнений

представив ее в виде матричного уравнения.

Решение. Перепишем систему в виде АХ=В, где

, ,

Решение матричного уравнения имеет вид .

Найдем :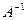

, , ,

, , ,

, ,

Таким образом , откуда

Следовательно, х=2, y=3, z=-2.

Поиск по сайту: