Ранг матрицы. Рассмотрим матрицу А размера

Рассмотрим матрицу А размера . . Выделим в ней k строк и k столбцов (). Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются минорами этой матрицы.

Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Обозначается r, r(A), rangA.

Очевидно, что , где - меньшее из чисел m и n.

Минор, порядок которого определяет ранг матрицы, называется базисным.

У матрицы может быть несколько базисных миноров.

Пример 1. Дана матрица . Определить ее ранг.

Решение. Имеем , , . Минор 4-го порядка составить нельзя.

Ответ: rangA=3.

Матрицы, имеющие одинаковый ранг, называются эквивалентными. Эквивалентность матриц обозначается знаком ~ между ними. Записывается А~В.

Надо отметить, что равные матрицы и эквивалентные матрицы - понятия совершенно различные.

Отметим свойства ранга матрицы:

1. При транспонировании матрицы ее ранг не меняется.

2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.

3. Ранг матрицы не изменится при элементарных преобразованиях матрицы.

Элементарными преобразованиями называются такие преобразования, при которых миноры матрицы либо не меняют своей величины, либо, меняя величину, не обращаются в нуль.

Элементарные преобразования матриц позволяют:

1. Переставлять местами между собой строки (столбцы).

2. Прибавлять к какой-либо строке (столбцу) другую строку (столбец), умноженную на любое число.

3. Умножать строку (столбец) на число, отличное от нуля.

4. Вычеркивать строки (столбцы), состоящие из одних нулей.

Простейший способ определения ранга матрицы состоит в приведении ее к ступенчатому виду при помощи последовательности элементарных преобразований.

Для этого необходимо с помощью элементарных преобразований привести исходную матрицу к диагональному виду

Пример 2. Определить ранг матрицы.

~ ~ , rangA = 2.

Пример 3. Определить ранг матрицы

Переставим первый и второй столбец местами:

~

Чтобы иметь дело с меньшими числами, умножим первый столбец на ~

Первую строку прибавляем ко второй и третьей, умножая при этом на (-2) и на (-1) соответственно: ~ .

Умножим вторую строку на , получим: ~ .

Умножим вторую строку на (-2) и прибавим ее к третьей строке: ~ .

Вычеркиваем третью строку: ~ .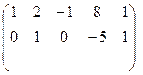

Отсюда видно, что ранг матрицы равен rang=2.

Контрольные вопросы

1. Какая матрица называется обратной по отношению к данной?

2. Каков порядок вычисления обратной матрицы?

3. Что называется рангом матрицы?

4. Какая матрица называется невырожденной?

5. Перечислите свойства обратной матрицы.

Занятие 6 (лекция)

Поиск по сайту: