 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Действия над матрицами
Содержание
| Занятие 1. (лекция) Матрицы | |
| Занятие 2. (практическое) Действия над матрицами | |
| Занятие 3. (лекция) Определители | |
| Занятие 4 (практическое) Вычисление определителя n-го порядка | |
| Занятие 5. (лекция) Обратная матрица. Ранг матрицы | |
| Занятие 6. (лекция) Системы линейных уравнений | |
| Занятие 7. (практическое) Решение системы линейных уравнений | |
| Занятие 8. Контрольная работа | |
| Литература |
Занятие 1 (лекция)
Тема: Матрицы
План:
- Матрицы. Основные понятия.
- Действия над матрицами.
2.1. Сложение.
2.2. Умножение на число
2.3. Произведение матриц.
Цели занятия:
На занятии вы узнаете
Ø Понятие матрицы, квадратной матрицы, треугольной матрицы, единичной матрицы, нулевой матрицы, транспонированной матрицы, противоположной матрицы, элементы матрицы, главной и побочной диагонали,
Ø Сложения матриц, умножение матрицы на число, произведение матриц,
Ø Свойства операции сложения матриц и умножения матрицы на число, произведения матриц,
Порядок работы на занятии:
- Прочитать текст лекции или прослушать лекцию преподавателя.
- Законспектировать лекцию.
- Ответить на контрольные вопросы, не заглядывая в конспект.
- Проверьте свои ответы по конспекту.
- Если ответы ошибочны, еще раз прочитайте лекцию и ответьте на контрольные вопросы. Будьте готовы к устному опросу и к применению знаний на практических занятиях.
Матрицы. Основные понятия
Алгебра – одна из составных частей современной математики. Название алгебра происходит от названии книги арабского математика Мухаммеда аль Хорезми «Ал-д жабр…»
Основной задачей алгебры было решение алгебраических уравнений, а так же систем уравнений и как особо важный случай, систем линейных уравнений. Для решения последних были введены понятия матрицы и определители, которые в последствии стали самостоятельными объектами изучения. Указанный материал впоследствии стал относиться к высшей алгебре.
Матрицей называется множество чисел, образующих прямоугольную таблицу, которая содержит m строк и n столбцов.
Матрица записывается в виде  или, сокращенно А =
или, сокращенно А =  ,
,
где i=1, 2, 3,…,m означает номер строки, j=1,2,3,…,n – номер столбца.
Матрицу А называют матрицей размера m×n и пишут 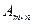 . Числа
. Числа 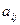 , составляющие матрицу, называются ее элементами.
, составляющие матрицу, называются ее элементами.
Матрицы равны между собой, если равны соответствующие элементы этих матриц, т.е. А=В, если 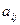 =
=  , где i=1,2,3,…,m, j=1,2,3,…,n
, где i=1,2,3,…,m, j=1,2,3,…,n
Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера  называют матрицей n-го порядка.
называют матрицей n-го порядка.
Рассмотрим квадратную матрицу порядка n: 
Элементы, стоящие на диагонали, идущей из левого верхнего угла  , образуют главную диагональ, а элементы, стоящие на диагонали, идущей из правого верхнего угла
, образуют главную диагональ, а элементы, стоящие на диагонали, идущей из правого верхнего угла  , образуют побочную диагональ.
, образуют побочную диагональ.
Пример.  - квадратная матрица 3-го порядка.
- квадратная матрица 3-го порядка.
Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.
Пример. А=  диагональная матрица n-го порядка.
диагональная матрица n-го порядка.
Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой Е.
Пример.  единичная матрица 3-го порядка.
единичная матрица 3-го порядка.
Матрица, все элементы которой равны нулю, называется нулевой.
Нулевая матрица обозначается буквой О. Имеет вид О = 
Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка соответственно). А=  В=
В= 
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается  . Транспонированная матрица обладает следующим свойством:
. Транспонированная матрица обладает следующим свойством:  .
.
Так, если  , то
, то 
Действия над матрицами
2.1.Сложение матриц
Поиск по сайту: