ОСНОВНЫЕ ЭТАПЫ СИНТЕЗА РЕГУЛЯТОРА ПОЛОЖЕНИЯ

Для синтеза регулятора положения (РП) применяют различные методы. Одним из них является синтез с применением ЛЧХ на основе критерия динамической точности системы при воспроизведении задающего гармонического воздействия [2]. Этот метод получил широкое применение при решении задач проектирования благодаря высокой степени наглядности и удобству интерпретации результатов вычислений.

Для обеспечения точности воспроизведения задающего гармонического воздействия:

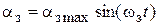(4.1)

необходимо, чтобы низкочастотная асимптота желаемой ЛЧХ проходила не ниже контрольной точки А _к. Ордината контрольной точки
на известной частоте 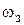задающего воздействия будет зависеть от ошибки

, (4.2)

где – передаточная функция скорректированного ЭП (рис. 4.1).

Рис. 4.1. Запретная область для астатических систем

При гармоническом входном сигнале (4.1) максимальная ошибка определится из (4.2):

.

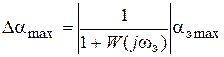В зоне рабочих частот >>1 и

,

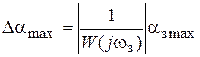откуда находим

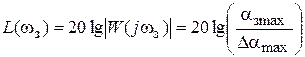. (4.3)

Выражение (4.3) может быть преобразовано, если заданы максимальные значения угловой скорости 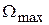и углового ускорения .

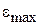При воспроизведении задающего воздействия (4.1) изменение угловой скорости и ускорения исполнительного вала ЭП определится через соответствующие производные:

;

.

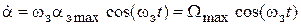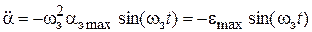Тогда координаты контрольной точки А _к вычисляются по формулам:

; .

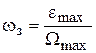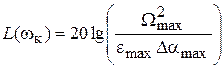Линии, образующие «запретную область» (рис. 4.1) получаются следующим образом: если зафиксировать значение 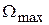, а амплитуду углового ускорения уменьшать, то контрольная точка А _к будет перемещаться влево от частоты 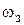по прямой с наклоном –20 Дб/дек; если теперь зафиксировать значение и уменьшать амплитуду угловой скорости 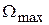, то контрольная точка А _к будет перемещаться вправо
от частоты 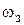по прямой с наклоном –40 Дб/дек.

Точка пересечения этой прямой с осью частот называется базовой частотой и вычисляется по формуле:

, (4.4)

где 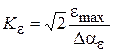– коэффициент передачи системы по ускорению;

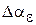– максимальное значение ошибки по ускорению.

Точка пересечения прямой с наклоном –20 Дб/дек с осью частот соответствует частоте, равной коэффициенту передачи системы
по скорости:

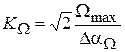, (4.5)

где 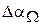– максимальное значение ошибки по скорости.

Таким образом, повышение точности отработки задающего воздействия обеспечивается коэффициентом передачи системы, что,
в свою очередь, может привести к уменьшению запасов устойчивости и
к увеличению числа колебаний переходного процесса. Колебательность системы оценивается показателем колебательности, который вычисляется по формуле:

,

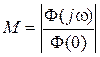где 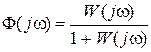– передаточная функция замкнутой системы.

В общем случае показатель колебательности должен лежать
в пределах: М = 1,1 ¸ 1,5. В следящих электроприводах часто, с целью демпфирования процесса слежения, требования к показателю колебательности ограничивают до величины: М = 1,1 ¸ 1,3.

Рассмотрим порядок синтеза РП с применением моделирующей программы в следящем ЭП.

Сформулируем основные этапы синтеза:

1. Обоснование структуры и расчет параметров желаемой передаточной функции 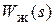ЭП.

2. Определение динамической модели неизменяемой части ЭП и преобразование передаточной функции 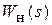для моделирования.

3. Составление алгоритма структурных преобразований по формуле:

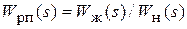
и построение ЛАЧХ РП.

4. Определение по ЛАЧХ структуры РП и расчет параметров передаточной функции РП.

5. Моделирование ССДМ ЭП с синтезированным РП и проверка соответствия полученных результатов техническим требованиям задания.

На первом этапе, при формировании желаемой передаточной функции 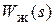необходимо исходить из требований к точностным характеристикам и динамическим показателям ЭП, которые сформулированы в техническом задании.

При разработке следящего ЭП с астатизмом второго порядка (n = 2) желаемая передаточная функция будет иметь вид:

. (4.6)

Низкочастотный участок желаемой ЛАХ 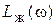пройдет через контрольную точку А _к с наклоном –40 Дб/дек и пересечет ось частот
на базовой частоте 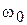(рис. 4.1). Протяженность среднечастотного участка желаемой ЛАХ зависит от постоянных времени и 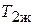, которые рассчитываются по формулам:

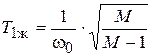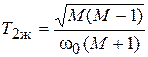; . (4.7)

При разработке следящего ЭП с астатизмом первого порядка (n = 1) желаемая передаточная функция будет иметь вид:

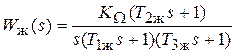. (4.8)

Первый участок желаемой ЛАХ 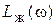, соответствующий передаточной функции (4.8) будет иметь наклон –20 Дб/дек (рис. 4.1). Поэтому на частоте 1/ график 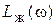системы с астатизмом первого порядка будет иметь излом, который желательно иметь в контрольной точке А _к. Для того чтобы система с передаточной функцией (4.8) имела максимальный запас по фазе, необходимо, чтобы соответствующая частота значительно превышала первую частоту сопряжения желаемой ЛАХ, т.е.:

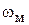>> 1/ . (4.9)

Частота, соответствующая максимальному запасу по фазе, зависит
от протяженности среднечастотного участка желаемой ЛАХ h и рассчитывается по формуле:

,

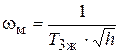где .

Если условие (4.9) выполняется, то расчет постоянных времен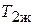и и 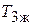в выражении (4.8) производится по формулам:

; . (4.10)

На втором этапе необходимо получить динамическую модель неизменяемой части ЭП в виде, удобном для моделирования. Неизменяемая часть ЭП представляет собой произведение передаточных функций: замкнутого контура скорости 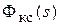, редуктора 1/ is и датчика положения К _дп.

Так как контур скорости настроен на оптимум по модулю,
то передаточная функция замкнутого контура может быть записана в виде:

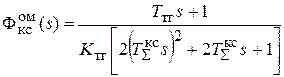. (4.11)

Содержание третьего этапа зависит от того, какое решение принято
о структуре желаемой передаточной функции .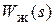

На четвертом этапе составляется алгоритм структурных преобразований согласно формуле:

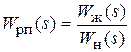(4.12)

и определяются ЛАЧХ регулятора положения. На этом этапе производится аппроксимация асимптотами полученных ЛАЧХ, определяется структура и рассчитываются параметры регулятора положения.

На последнем этапе исследуется полная динамическая модель синтезированного ЭП при различных типовых воздействиях с целью подтверждения правильности расчетов и проверки соответствия полученных результатов техническим требованиям задания.

Поиск по сайту: