АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

ДИНАМИЧЕСКИЕ СВОЙСТВА ДВИГАТЕЛЯ ПОСТОЯННОГО ТОКА С ЯКОРНЫМ УПРАВЛЕНИЕМ

Читайте также:
  1. F. Метод, основанный на использовании свойства монотонности показательной функции .
  2. I. Размеры и тинкториальные свойства волокон
  3. II. Свойства векторного произведения
  4. III. Психические свойства личности – типичные для данного человека особенности его психики, особенности реализации его психических процессов.
  5. IV) Ферродинамические измерительные механизмы
  6. IV. Относительные величины, динамические ряды
  7. V2: Законы постоянного тока
  8. V2: Электрические и магнитные свойства вещества
  9. Агрегатные состояния и термодинамические фазы
  10. Аденовирусы, морфология, культуральные, биологические свойства, серологическая классификация. Механизмы патогенеза, лабораторная диагностика аденовирусных инфекций.
  11. Аксиомы ординалистского подхода. Функция полезности и кривые безразличия потребителя. Свойства кривых безразличия. Предельная норма замещения
  12. Акустические свойства голоса

Динамические свойства силового канала ЭП с двигателем для выходного напряжения блока питания описываются уравнением электрического равновесия:

. (1.1)

Коэффициент противо-ЭДС К е вычисляется при номинальных значениях параметров:

; ; ,

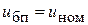поэтому

,

откуда

. (1.2)

Для вывода динамической модели двигателя необходимо уравнение (1.1) дополнить уравнением механического равновесия:

, (1.3)

где – суммарный момент инерции двигателя и нагрузки, приведенный к валу двигателя.

Первое слагаемое в правой части уравнения (1.3) характеризует вращающий момент двигателя:

.

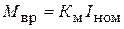Коэффициент момента рассчитывается по моментной характеристике двигателя (рис. 1.2) при номинальных значениях момента вращения и тока якоря :

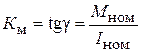. (1.4)

Рис. 1.2. Моментная характеристика двигателя

Для построения структурной схемы динамической модели (ССДМ) двигателя, запишем уравнения (1.1) и (1.3) в операторной форме и преобразуем их:

; (1.5)

, (1.6)

где электромагнитная постоянная времени и электромеханическая постоянная времени .

Из (1.5) получим:

. (1.7)

На основании (1.6) и (1.7) построим ССДМ, изображенную на рис. 1.3.

 

Рис. 1.3. Структурная схема динамической модели двигателя


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)