УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СТАЦИОНАРНЫХ СИСТЕМ

В современной теории управления широко применяется метод пространства состояний, который базируется на математических моделях в переменных состояния [4, 5, 6, 7, 8, 10, 12, 13]. Такая математическая модель представляет собой систему уравнений первого порядка, которую обычно представляют в векторно-матричной форме. Преимущество такого представления заключается в том, что облегчается решение задач анализа и синтеза с применением ЦВМ на этапе проектирования.

Динамические свойства линейной непрерывной стационарной системы описываются векторно-матричными уравнениями:

, (3.1)

, (3.2)

где x ^T = [ x₁ x₂... x_n ] – вектор-состояния размерности (n ´1);

u ^T = [ u₁ u₂... u_m ] – вектор-входа размерности (m ´1);

y ^T = [ y₁ y₂... y_q ] – вектор-выхода размерности (q ´1);

A, B, C и D – матрицы коэффициентов размерности (n ´ n), (n ´ m), (q ´ n), (q ´ m), соответственно.

Уравнение (3.1) связывает переменные состояния и входные переменные и называется уравнением состояния. Уравнение (3.2) связывает выходные переменные с переменными состояния и входными переменными, и называется уравнением выхода.

На рис. 3.1 изображена векторная структурная схема линейной непрерывной стационарной системы, построенная по уравнениям (3.1) и (3.2).

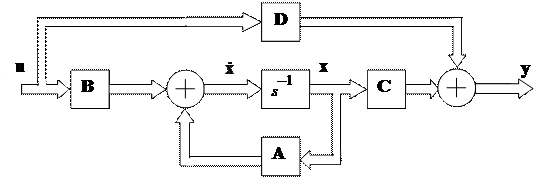
Рис. 3.1. Векторная структурная схема

Из схемы следует, что на выходе интегратора (s ^–1) формируется вектор состояния x. Матрица A называется основной матрицей системы;
B – матрица связи вектора входа системы с переменными состояния;
C – матрица связи переменных состояния с вектором выхода системы;
D – матрица связи вектора входа с вектором выхода.

Поиск по сайту: