КОНТУРА СКОРОСТИ

Пример 3.1. Провести дискретную аппроксимацию регулятора скорости, синтезированного в примере 2.1 с применением формулы трапеций и метода непосредственного программирования. Для расчетов принять период квантования Т ₀ = 0,001 с.

Решение. Преобразуем передаточную функцию регулятора скорости

,

к виду

.

Параметр .

1. С помощью формулы трапеций определим

Тогда

. (3.19)

Заметим, что переход к z -преобразованию с применением MatLab предусматривает деление на коэффициент при старшей степени z
в знаменателе. В нашем случае коэффициент при z ²

.

Тогда в выражении (3.19)

; ; ;

;

;

.

Здесь = 0,06975 с; Т _рс1 = 0,0316 с; Т _рс2 = 0,04 с; Т _рс3 = 0,002 с.

2. Составляем структурную схему программирования (см. рис. 3.2), которой соответствуют уравнения (3.8) – (3.12).

По уравнениям состояния и выхода определяем коэффициенты матриц А, B, C, D, соответственно:

; ; ; .

Пример 3.2. Составить ССДМ КС с цифровым регулятором скорости и получить переходные характеристики по управляющему и возмущающему воздействиям. Провести анализ результатов моделирования.

Параметры двигателя, БП, ТГ и цифрового регулятора принять
из примеров 1.1, 2.1, 3.1. Коэффициент передачи АЦП К_{VZ 2} = 1.

Решение. 1. Для моделирования построим ССДМ КС с цифровым регулятором скорости в системе Simulink (рис. 3.6).

Рис. 3.6. Структурная схема динамической модели контура скорости

с цифровым регулятором скорости

Цифровой регулятор скорости реализован блоком Discrete State-Space, расположенным в библиотеке блоков Discrete. Диалоговое окно блока представлено на рис. 3.7.

Рис. 3.7. Диалоговое окно блока Discrete State-Space

Блок Zero-Order Hold представляет собой экстраполятор нулевого порядка, восстанавливающий непрерывный сигнал u _рс с выхода цифрового регулятора скорости. Блок Switch реализует модель квантователя, преобразующего непрерывный сигнал рассогласования∆ u _W в дискретный. Блок Pulse Generator формирует последовательность единичных импульсов с периодом следования Т ₀.

Для задания параметров блока Zero-Order Hold необходимо –
в строке Sample time установить период квантования Т ₀ (рис. 3.8).

Рис. 3.8. Диалоговое окно блока Zero-Order Hold

Для задания параметров блока Pulse Generator необходимо – в строке Period установить период квантования Т ₀ (рис. 3.9).

Рис. 3.9. Диалоговое окно блока Pulse Generator

2. Для получения графика в блоке Step задаем входное воздействие В, а в блоке Step1 значение момента сопротивления .

На рис. 3.10 изображена переходная характеристика контура скорости по управляющему воздействию. Время моделирования составляет 0,2 с.

Для построения переходной характеристики по моменту сопротивления нагрузки 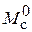устанавливаем в блоке Step входное воздействие , а в блоке Step 1 момент сопротивления . Результаты моделирования представлены на рис. 3.11.

W(t), рад/с

t, c

Рис. 3.10. Переходная характеристика контура скорости по управляющему воздействию

W(t), рад/с

t, c

Рис. 3.11. Переходная характеристика контура скорости по моменту

сопротивления

3. Переходим к анализу полученных графиков. По характеристике
на рис. 3.10 определяем максимальное значение угловой скорости вращения ЭД W_max = 336 рад/с и установившееся значение W_уст = 314 рад/с. По этим данным рассчитываем перерегулирование:

.

Время нарастания 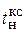составляет: 0,0245 с.

Проверяем соответствия требованиям настройки на ОМ:

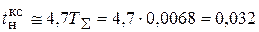с.

Анализ полученных результатов показывает, что дискретная аппроксимация регулятора скорости привела к уменьшению запасов устойчивости, поэтому перерегулирование s увеличилось, а время нарастания 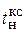уменьшилось по сравнению с аналоговой моделью регулятора скорости.

Пример 3.3. Построить график ЛЧХ разомкнутого КС. Провести анализ результатов моделирования. Для расчетов принять период квантования Т ₀ = 0,02 с.

Решение. Для построения частотных характеристик к выражению (2.25) применим z -преобразование в соответствии с формулой трапеций. Числовые значения коэффициентов разомкнутого контура скорости получены в примере 2.1 (программа построения ЛЧХ).

Программа для перехода переменной z записывается в Command Window следующим образом:

num=[0.006483 0.1621 5.129];

den=[9.522e-013 1.347e-009 6.336e-007 0.0001043 0.00268 0.0698 0];

fs=500;

[numd, dend]=bilinear(num, den, fs)

numd =

0.0022 0.0045 -0.0018 -0.0085 -0.0024 0.0041 0.0021

dend =

1.0000 -4.0669 6.6020 -5.4346 2.3765 -0.5222 0.0451

В приведенной программе частота дискретизации:

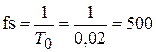Гц.

Полученные численные значения позволяют записать передаточную функцию разомкнутого контура скорости относительно переменной z:

,

где b ₆= 0,0022; b ₅= 0,0045; b ₄= – 0,0018; b ₃= – 0,0085; b ₂= – 0,0024;

b ₁= 0,0041; b ₀= 0,0021;

d ₆= 1,0; d ₅= – 4,0669; d ₄= 6,6020; d ₃= – 5,4346; d ₂= 2,3765; d ₁= – 0,5222; d ₀= 0,0451.

К полученному выражению применим -преобразование (3.15):

.

После вычисления коэффициентов при переменной u и приведения
к стандартному виду, получим:

.

Далее переходим к построению логарифмических псевдочастотных характеристик (ЛПЧХ) в соответствии с программой:

w = logspace(–3, 3);

num = [0 2 2 -2 1372 34 2];

den = [200473 283592 133397 21960 563 16 -1];

bode(num, den, w)

Результаты моделирования представлены на рис. 3.12.

Рис. 3.12. Логарифмические псевдочастотные характеристики

контура скорости

Как и следовало ожидать, при увеличении перерегулирования
(см. пример 3.2) запасы устойчивости по фазе и амплитуде уменьшились по сравнению с аналоговым контуром скорости. Так, запас устойчивости по фазе на псевдочастоте среза равен:

,

а запас устойчивости по амплитуде на псевдочастоте равен:

дБ.

При переходе к абсолютной псевдочастоте среза

с^{– 1},

а частота

с^{– 1}.

Графики ЛПЧХ сдвигаются вправо относительно оси частот
на величину , при этом запасы устойчивости по фазе и амплитуде останутся прежними.

Поиск по сайту: