Настройка на симметричный оптимум

Настройкой контура на СО называется синтез регулятора с целью получения динамических характеристик контура, близких к типовым характеристикам контура с астатизмом второго порядка (), перерегулированием, равным 43 %, запасом устойчивости по фазе и временем нарастания переходного процесса t _{н .}

В основе процедуры настройки на СО лежит допущение о том, что
в рабочем диапазоне частот выражение (2.5), с учетом:

>> 1, (2.13)

можно представить в виде:

= . (2.14)

Применительно к ССДМ КС (рис. 2.1) передаточная функция неизменяемой части:

= . (2.15)

Для получения желаемых результатов нужно выбрать ПИ-регулятор (2.10) с параметрами:

и = .

Тогда передаточная функция КС, настроенного на СО:

= . (2.16)

Из выражения (2.16) видно, что свойства КС соответствуют свойствам контура с астатизмом 2-го порядка. Динамические свойства КС иллюстрируются графиками (рис. 2.4, 2.5). Показатели качества КС, настроенного на СО, имеют следующие значения: 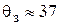º, перерегулирование = 43 % и время нарастания переходного процесса
t _н 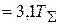= 0,31 с.

Рис. 2.4. Переходная характеристика при настройке на симметричный оптимум

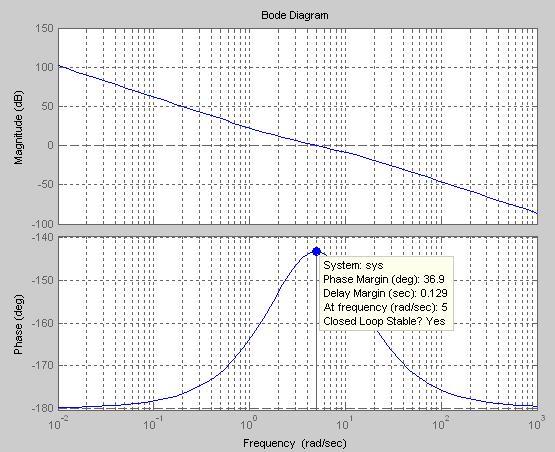
Рис. 2.5. Стандартный график ЛЧХ при настройке на симметричный оптимум

Если условие (2.13) трудновыполнимо, то производят настройку КС с передаточной функцией (2.9). Параметры ПИ-регулятора, при этом, рассчитываются по выражениям:

и Т _рс = .

Тогда передаточная функция скорректированного КС:

= . (2.17)

Следует отметить, что в полученном выражении необходимым является выполнение условия > 4 , в противном случае настройка
на СО невозможна.

Выбирая для примера КС, структурная схема которого представлена на рис. 2.1, Т _м = 0,1 с, получаем ЛЧХ и переходную характеристику КС (рис. 2.6, 2.7), с астатизмом первого порядка ( = 1).

Рис. 2.6. ЛЧХ контура скорости с астатизмом первого порядка

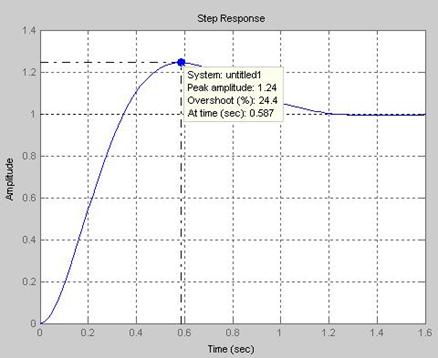
Рис. 2.7. Переходная характеристика контура скорости

с астатизмом первого порядка

Также заметим, что при увеличении электромеханической постоянной времени Т _м и неизменном значении суммарной малой постоянной времени увеличивается запас по фазе º и уменьшается перерегулирование %.

Поиск по сайту: