Настройка на оптимум по модулю

Настройкой контура на ОМ называется синтез регулятора с целью получения динамических характеристик замкнутого контура, близких
к характеристикам колебательного звена с относительным коэффициентом затухания = = 0,707, перерегулированием = 4,3 %, запасом устойчивости по фазе º, временем нарастания 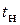= 4,7 Т _Σ.

При настройке контура на ОМ осуществляется компенсация больших постоянных времени силового канала ЭП и динамические процессы будут определяться суммарными малыми постоянными времени 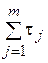контура.

Любой контур считается настроенным на ОМ, если его передаточная функция в разомкнутом состоянии имеет вид:

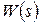= , (2.1)

где

= .

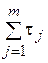Рассмотрим синтез регулятора применительно к неизменяемой части ЭП, которая описывается передаточной функцией:

= , (2.2)

где Т_i – компенсируемые большие постоянные времени контура.

При выполнении условия:

Т _i >> 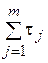, (2.3)

второй сомножитель (2.2) можно записать как:

, (2.4)

тогда передаточная функция неизменяемой части ЭП:

= . (2.5)

При последовательной коррекции передаточная функция регулятора:

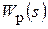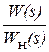= . (2.6)

После подстановки в (2.6) выражений (2.1) и (2.5) получим:

= ,

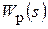или

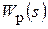= , (2.7)

где К _p = ; ; Т _p – параметры регулятора.

В качестве примера настройки на ОМ, рассмотрим настройку контура скорости (КС). ССДМ КС изображена на рис. 2.1.

Рис. 2.1. Структурная схема динамической модели контура скорости

Передаточная функция неизменяемой части КС запишется в виде произведения передаточных функций блока питания, двигателя и тахогенератора:

= .

Электромеханическая постоянная времени двигателя Т _м является постоянной времени, подлежащей компенсации.

Постоянные времени блока питания (БП) Т _бп и тахогенератора (ТГ) Т _тг являются малыми постоянными времени, и их влияние сказывается на высоких частотах, поэтому произведение инерционных звеньев с малыми постоянными времени можно заменить одним инерционным звеном:

, (2.8)

где = Т _бп + Т _тг – суммарная малая постоянная времени КС.

С учетом приближения выражение (2.8) примет вид:

= . (2.9)

С применением формулы (2.6) определяем передаточную функцию регулятора скорости (РС):

,

где передаточная функция настроенного на ОМ разомкнутого КС:

. (2.10)

Тогда

= .

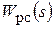Переписывая передаточную функцию РС в стандартном виде, получим:

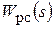= , (2.11)

где Т _рс = Т _м, а К _рс = .

Полученная передаточная функция РС описывает динамические свойства ПИ-регулятора.

Согласно (2.10), передаточная функция замкнутого КС:

= . (2.12)

Перепишем (2.12) как:

= ,

где Т _кс = – постоянная времени КС; = = 0,707.

На рис. 2.2, 2.3 показаны стандартные графики ЛЧХ и переходной характеристики при настройке на ОМ, полученные по выражениям (2.10) и (2.12). По графикам определяем показатели качества КС, настроенного
на ОМ: запас устойчивости по фазе º, перерегулирование = 4,32 % и время нарастания переходного процесса t _н = 0,47 с._.

Настройка на ОМ позволяет получить достаточное быстродействие при небольшом перерегулировании. В ряде случаев, когда требуется получить повышенное быстродействие и точность системы, применяют настройку на СО.

Рис. 2.2. Стандартный график ЛЧХ при настройке на оптимум по модулю

Рис. 2.3. Переходная характеристика при настройке

на оптимум по модулю

Поиск по сайту: