Средние величины

В медицине, в здравоохранении очень часто используются выражаемые числами признаки, которые могут принимать различные числовые значения у разных единиц совокупности, нередко повторяющиеся у нескольких единиц. В каждой данной совокупности и в данных конкретных условиях этот признак характеризуется определенной величиной (уровнем), которая отличается от величины этого признака в другой совокупности, при наличии других условий. Пульс, АД, температура тела, длительность временной нетрудоспособности, длительность пребывания в стационаре отличаются (варьируют) у больных даже с одним диагнозом.

Величину изучаемого признака могут принимать либо дискретные (прерывные), либо непрерывные числовые значения. Примеры дискретных величин, при которых значения выражены целыми числами: число детей в семье, число больных в палате, число койко-дней, число каких-либо медицинских аппаратов в учреждении, пульс. Примеры непрерывно изменяющихся величин, когда значения выражены дробными величинами, могут постепенно переходить одно в другое: рост, масса тела, температура, АД.

Полученные при исследовании величину сначала записывают хаотично, то есть в том порядке, как их получает исследователь. Ряд, в котором упорядочение сопоставлены (по степени возрастания или убывания) варианты и соответствующие им частоты, называется вариационным. Отдельные количественные выражения признака называются вариантами (V), а числа, показывающие, как часто эти варианты повторяются — частотами (Р).

Для обобщенной числовой характеристики изучаемого признака у совокупности обследуемых рассчитываются средние величины, достоинство которых заключается в том, что одна величина характеризует большую совокупность однородных явлений.

Различают несколько видов средних величин: средняя арифметическая, средняя геометрическая, средняя гармоническая, средняя прогрессивная, средняя хронологическая. Кроме указанных средних, иногда в качестве обобщающих величин вариационного ряда используют особые средние относительного характера — моду и медиану.

Мода (Мо) — наиболее часто повторяющаяся варианта. Медиана (Me) —значение варианты, делящей вариационный ряд пополам; по обе стороны от нее находится равное число вариант.

Наиболее часто используется средняя арифметическая. Средняя арифметическая, которая рассчитана в вариационной ряду, где каждая варианта встречается только один раз (или все варианты встречаются с одинаковой частотой) называется средней арифметической простой. Она определяется по формуле:

М — средняя арифметическая;

V — значение вариационного признака;

n — общее число наблюдений.

Если в исследуемом ряду одна или несколько вариант повторяются, то вычисляют среднюю арифметическую взвешенную. При этом учитывается вес каждой варианты и, чем большую частоту имеет данная варианта, тем больше будет ее влияние на среднюю арифметическую. Расчет такой средней производится по формуле:

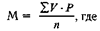
Р — частота;

п — сумма частот.

Пример составления вариационного ряда и расчета основных его характеристик представлен в таблице 5.8.

Таблица 5.1

Поиск по сайту: