Рівняння Слуцького

Вектор - вектор споживання – показує кількість товарів, що ми купили.

- вектор цін.

- бюджет;

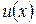- функція корисності від .

Функція корисності 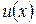має такі властивості:

1) вона є неперервно-диференційована, тобто існує похідна по кожному з товарів.

2) має додатні перші частинні похідні її всіма змінними (функція зростаюча) .

3) має від’ємно-визначену матрицю Гессе других частинних похідних.

Неокласична задача споживача:

При заданих цінах і фіксованому доході бюджетне обмеження в буде лінійним, а тому розв’язок моделі існує і він буде єдиним.

Розв’яжемо методом Лагранжа:

Теорема Куна-Таккера.

- оптимальний розв’язок моделі , тоді і тільки тоді, коли існує , що є сідловою точкою функції Лагранжа. Тобто, .

Застосуємо теорему Куна-Таккера.

З умови 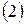, ми можемо визначити граничну корисність в точці для -го товару:

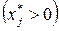Якщо припустити, що -й товар споживають , то виконується така рівність:

Оскільки при виконується і , то 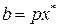, тобто хнаходиться на бюджетному обмеженні.

Припустимо, що індивід купує всі товарів: . Тоді, 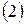можна переписати в спрощеному вигляді:

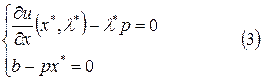
Умова - це умова 1-го роду для неокласичної задачі споживання.

Застосовуючи метол порівняльної статистики необхідно вивчити чутливість розв’язку задачі при зміні параметрів і , шляхом порівняння положення оптимуму до і після зміни параметрів.

Аналіз:

1) Проаналізуємо вплив зміни доходу на розв’язок неокласичної задачі. Для цього ми продиференціюємо по :

2) Визначимо вплив зміни ціни на розв’язок задачі. Для цього ми продиференціюємо по :

3) Визначимо вплив компенсованої зміни ціни на розв’язок:

Основне матричне рівняння теорії вибору:

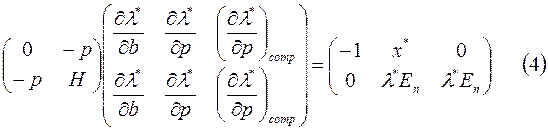
- матриця порівняльної статистики. ЇЇ елементи – показники порівняльної статики.

З рівняння можна отримати рівняння Слуцького у векторній формі:

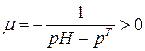- можна проінтерпретувати, як коефіцієнт спадання граничної корисності грошей.

Твердження:

Рівняння називається рівнянням Слуцького, або основним рівнянням теорії цінностей. У векторній формі рівняння Слуцького виглядає так:

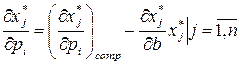
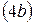
Ліву частину рівняння 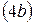називають загальним ефектом.

- називають ефектом заміщення. - називають ефектом доходу.

З рівняння Слуцького можна отримати класифікацію товарів.

Якщо - товар Гіфена, 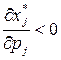- нормальний товар;

Якщо - звичайний товар, - товар низької якості;

- товари замінники;

- товари доповнення;

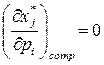- товари не пов’язані;

Рівняння Слуцького:

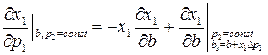
Рівняння Хікса:

Висновки:

1. Криві дохід-споживання в графічному виражені показують як споживання товарів змінюється при зміні доходу. При цьому виділяємо нормальні товари ( при ), товари низької якості ( при ).

2. Криві Енгеля показують співвідношення між грошовим доходом та кількістю товару, що споживається. Криві Енгеля для нормальних товарів мають зростаючий попит.

3. В аналізі реакції споживача на зміну цін важливо враховувати вплив на споживацькі стимули. Ефект доходу означає, що зниження ціни дає змогу споживачеві придбати більшу кількість товару за тієї ж величини грошового доходу. Ефект заміщення вказує на те, що величини грошового доходу. Ефект заміщення вказує на те, що зниження ціни робить товар відносно більш привабливим і таким чином збільшує схильність споживача до заміщення цим товаром інших.

Поиск по сайту: