 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Стандартные теплоты (энтальпии) образования
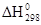 некоторых веществ
некоторых веществ
| Вещество | Состояние | 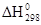 кДж/моль кДж/моль
| Вещество | Состояние | 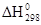 кДж/моль кДж/моль
|
| С2Н2 | г | +226,75 | СО | г | -110,52 |
| CS2 | г | +115,28 | СН3ОН | г | -201,17 |
| NO | г | +90,37 | С2Н5OН | г | -235,31 |
| С6Н6 | г | +82,93 | H2O | г | -241,83 |
| С2Н4 | г | +52,28 | Н2О | ж | -285,84 |
| H2S | г | -20,15 | NH4C1 | к | -315,39 |
| NН3 | г | -46,19 | СО2 | г | -393,51 |
| СН4 | г | -74,85 | Fе2О3 | к | -822,10 |
| С2Н6 | г | -84,67 | TiO2 | к | -943,90 |
| НС1 | г | -92,31 | Са(ОН)2 | к | -986,50 |
| А12O3 | к | -1669,80 |
Пример 2. Реакция горения этана выражается уравнением:
С2Н6(г) + 31/2О2= 2СО2(г)+3Н2О(ж); ∆Hх.р.= -1559,87 кДж
Вычислите теплоту образования этана, если известны теплоты образования СO2(г) и Н2O(ж) (см. табл. 15).
Решение. Теплотой образования (энтальпией) данного соединения называют тепловой эффект реакции образования 1 моль этого соединения из простых веществ, взятых в их устойчивом состоянии при данных условиях.
Обычно теплоту образования относят к стандартному состоянию, т.е. 25° С (298 К) и 1,013×105 Па и обозначают через 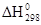 .Так как тепловой эффект с температурой изменяется незначительно, то в дальнейшем индексы опускаются и тепловой эффект обозначается через
.Так как тепловой эффект с температурой изменяется незначительно, то в дальнейшем индексы опускаются и тепловой эффект обозначается через  Н. Следовательно, нужно вычислить тепловой эффект реакции, термохимическое уравнение которой имеет вид
Н. Следовательно, нужно вычислить тепловой эффект реакции, термохимическое уравнение которой имеет вид
2С(графит)+3Н2(г) = С2Н6(г); ∆H =?
исходя из следующих данных:
а) С2Н6(г) + 31/2О2(г)=2СО2(г)+3Н2О(ж); ∆H =-1559,87 кДж
б) 2С(графит)+О2(г)= СО2(г); ∆H =-393,51 кДж
в) Н2(г)+ 1/2О2=Н2О(ж); ∆H =-285,84 кДж
На основании закона Гесса с термохимическими уравнениями можно оперировать так же, как и с алгебраическими. Для получения искомого результата следует уравнение (б) умножить на 2, уравнение (в) — на 3, а затем сумму этих уравнений вычитают из уравнения (а):
С2Н6 + 31/2О2-2С-2О2-3Н2-3/2О2=2СО2+3Н2О-2СО2-3Н2О
∆H =-1559,87-2(-393,51)-3(-285,84)= +84,67 кДж;
∆H =-1559,87+787,02+857,52;
С2Н6=2С+3Н2; ∆H = +84,67 кДж
Так как теплота образования равна теплоте разложения с обратным знаком, то 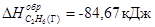 . К тому же результату придем, если для решения задачи применить вывод из закона Гесса:
. К тому же результату придем, если для решения задачи применить вывод из закона Гесса:
∆Hх.р. =2∆Hсо2+3∆Hн2о-∆Hс2н6-31/2∆Hо2
Учитывая, что теплоты образования простых веществ условно приняты равными нулю
∆Hс2н6=2∆Hсо2+3∆Hн2о-∆Hх.р.
∆Hс2н6=2(-393,51)+3(-258,84)+1559,87=-84,67;
∆Hобрс2н6(г)=-84,67 кДж
Пример 3. Реакция горения этилового спирта выражается термохимическим уравнением
С2Н5ОН(ж)+3О2(г)=2СО2(г)+3Н2О(ж); ∆H=?
Вычислите тепловой эффект реакции, если известно, что молярная теплота парообразования С2Н5OН(ж) равна +42,36 кДж, а теплоты образования С2Н5OН(г), СO2(г), Н2O(ж) см. табл. 15.
Решение. Для определения  Н реакции необходимо знать теплоту образования С2Н5OН(ж). Последнюю находим из данных:
Н реакции необходимо знать теплоту образования С2Н5OН(ж). Последнюю находим из данных:
С2Н5ОН(ж) = С2Н5ОН(г); ∆H = + 42,36 кДж
+42,36 = - 235,31- ∆Hс2н5он (ж);
∆Hс2н5он (ж) = - 235,31-42,36 = -277,67 кДж
Вычисляем  H реакции, применяя следствие из закона Гесса:
H реакции, применяя следствие из закона Гесса:
∆Hх.р.=2(-393,51)+3(-285,84)+277,67=-1366,87 кДж
5.5. Химическое сродство. Энтропия химических реакций. Энергия Гиббса. Самопроизвольно могут протекать реакции, сопровождающиеся не только выделением, но и поглощением теплоты.
Реакция, идущая при данной температуре с выделением теплоты, при другой температуре проходит с поглощением теплоты. Здесь проявляется диалектический закон единства и борьбы противоположностей. С одной стороны, система стремится к упорядочению (агрегации), к уменьшению Н; с другой стороны, система стремится к беспорядку (дезагрегации). Первая тенденция растет с понижением, а вторая — с повышением температуры. Тенденцию к беспорядку характеризует величина, которую называют энтропией.
Энтропия S, так же как внутренняя энергия U, энтальпия Н, объем V и др., является свойством вещества, пропорциональным его количеству. S, U, H, V обладают аддитивными свойствами, т.е. при соприкосновении системы суммируются. Энтропия отражает движение частиц вещества и является мерой неупорядоченности системы. Она возрастает с увеличением движения частиц: при нагревании, испарении, плавлении, расширении газа, при ослаблении или разрыве связей между атомами и т.п. Процессы, связанные с упорядоченностью системы: конденсация, кристаллизация, сжатие, упрочнение связей, полимеризация и т.п.— ведут к уменьшению энтропии. Энтропия является функцией состояния, т.е. ее изменение  зависит только от начального (S1) и конечного (S2) состояний и не зависит от пути процесса:
зависит только от начального (S1) и конечного (S2) состояний и не зависит от пути процесса:
∆Sx.p.=∑S0прод - ∑S0исх
∆S=S2-S1
если S2>S1, то ∆S>0
если S2<S1, то ∆S<0 (2)
Так как энтропия увеличивается с повышением температуры, то можно считать, что мера беспорядка равна» T  S. Энтропия выражается в Дж/(моль.К).
S. Энтропия выражается в Дж/(моль.К).
Таким образом, движущая сила процесса складывается из двух сил: стремления к упорядочению (Н) и стремления к беспорядку (TS). При р = const и Т = const общую движущую силу процесса, которую обозначают  G, можно найти из соотношения
G, можно найти из соотношения
∆G=(H2-H1)-(TS2-TS1); ∆G=∆H-T∆S
где: величина G называется изобарно-изотермическим потенциалом или энергией Гиббса.
Мерой химического сродства является убыль энергии Гиббса ( G), которая зависит от природы вещества, его количества и температуры.
G), которая зависит от природы вещества, его количества и температуры.
Энергия Гиббса является функцией состояния, поэтому
∆Gx.p.=∑ ∆Goбpпрод-∑∆Goбpисх (3)
Самопроизвольно протекающие процессы идут в сторону уменьшения потенциала и, в частности, в сторону уменьшения  G. Если
G. Если  G < 0, процесс принципиально осуществим; если
G < 0, процесс принципиально осуществим; если  G>0, процесс самопроизвольно проходить не может. Чем меньше
G>0, процесс самопроизвольно проходить не может. Чем меньше  G, тем сильнее стремление к протеканию данного процесса и тем дальше он от состояния равновесия, при котором
G, тем сильнее стремление к протеканию данного процесса и тем дальше он от состояния равновесия, при котором  G = 0 и
G = 0 и  H= T
H= T  S.
S.
Из соотношения  G =
G =  H – T
H – T  S видно, что самопроизвольно могут протекать и процессы, для которых
S видно, что самопроизвольно могут протекать и процессы, для которых  H>0 (эндотермические). Это возможно, когда
H>0 (эндотермические). Это возможно, когда  S >0, но |T
S >0, но |T  S| > |
S| > |  H| и тогда
H| и тогда  G<0. С другой стороны, экзотермические реакции (
G<0. С другой стороны, экзотермические реакции ( H<0) самопроизвольно не протекают, если при
H<0) самопроизвольно не протекают, если при  S<0 окажется, что
S<0 окажется, что  G>0.
G>0.
5.6. Второй и третий законы термодинамики. Для систем, которые не обмениваются с окружающей средой ни энергией, ни веществом (изолированные системы), второй закон термодинамики имеет следующую формулировку: в изолированных системах самопроизвольно идут только такие процессы, которые сопровождаются возрастанием энтропии: AS > 0.
Второй закон термодинамики имеет статистический характер, т.е.
справедлив лишь для систем, состоящих из очень большого числа
частиц.
Однако, если в системе протекает химическая реакция, то система обменивается энергией с окружающей средой, т.е. не является изолированной. Химические реакции обычно сопровождаются изменением как энтропии, так и энтальпии.
В отличие от других термодинамических функций, можно определить не только изменение, но абсолютное значение энтропии. Это вытекает из высказанного в 1911 г. М. Планком постулата, согласно которому «при абсолютном нуле энтропия идеального кристалла равна нулю». Этот постулат получил название третьего закона термодинамики.
Пример 1. В каком состоянии энтропия 1 моль вещества больше при одинаковой температуре: в кристаллическом или парообразном?
Решение. Энтропия есть мера неупорядоченности состояния вещества. В кристалле частицы (атомы, ионы) расположены упорядоченно и могут находиться лишь в определенных точках пространства, а для газа таких ограничений нет. Объем 1 моль газа гораздо больше объема 1 моль кристаллического вещества; возможность хаотичного движения молекул газа больше. А так как энтропию можно рассматривать как количественную меру хаотичности атомно-молекулярной структуры вещества, то энтропия 1 моль паров вещества больше энтропии 1 моль его кристаллов при одинаковой температуре.
Пример 2. Прямая или обратная реакция будет протекать при стандартных условиях в системе
СН4(г)+СО2 ↔ 2СО(г)+2Н2(г)
Решение. Вычислим  прямой реакции. Значения
прямой реакции. Значения  соответствующих веществ приведены в табл. 16. Зная, что
соответствующих веществ приведены в табл. 16. Зная, что  G есть функция состояния и что
G есть функция состояния и что  G для простых веществ, находящихся в устойчивых при стандартных условиях агрегатных состояниях, равны нулю, находим
G для простых веществ, находящихся в устойчивых при стандартных условиях агрегатных состояниях, равны нулю, находим  процесса:
процесса:
∆G0298 = 2 (-137,27) +2 (0) - (-50,79-394,38) = +170,63 кДж
То, что  > 0, указывает на невозможность самопроизвольного протекания прямой реакции при Т = 298К и давлении взятых газов равном 1,013 ∙ 105 Па (760 мм рт. ст. = 1 атм).
> 0, указывает на невозможность самопроизвольного протекания прямой реакции при Т = 298К и давлении взятых газов равном 1,013 ∙ 105 Па (760 мм рт. ст. = 1 атм).
Таблица 16
Стандартная энергия Гиббса образования  некоторых веществ
некоторых веществ
| Вещество | Состояние |  , кДж/моль , кДж/моль
| Вещество | Состояние |  , кДж/моль , кДж/моль
|
| ВаСО3 | к | -1138,8 | FeO | к | -244,3 |
| СаСО3 | к | -1128,75 | Н2О | ж | -237,19 |
| Fе3O4 | к | -1014,2 | Н2O | г | -228,59 |
| ВеСО3 | к | -944,75 | PbO2 | к | -219,0 |
| СаО | к | -604,2 | СО | г | -137,27 |
| ВеО | к | -581,61 | СН4 | г | -50,79 |
| NaF | к | -541,0 | NO2 | г | +51,84 |
| ВаО | к | -528,4 | NO | г | +86,69 |
| СО2 | г | -394,38 | C2H2 | г | +209,20 |
| NaCl | к | -384,03 | |||
| ZnO | к | -318,2 |
Таблица17
Стандартные абсолютные энтропии 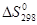 некоторых веществ
некоторых веществ
| Вещество | Состояние | 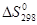 , Дж/(моль.К) , Дж/(моль.К)
| вещество | Состояние | 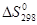 ,Дж/(моль.К) ,Дж/(моль.К)
|
| С | Алмаз | 2,44 | Н2O | г | 188,72 |
| С | Графит | 5,69 | N2 | г | 191,49 |
| Fe | к | 27,2 | NН3 | г | 192,50 |
| Ti | к | 30,7 | СО | г | 197,91 |
| S | Ромб | 31,9 | с2H2 | г | 200,82 |
| TiO2 | к | 50,3 | O2 | г | 205,03 |
| FeO | к | 54,0 | H2S | г | 205,64 |
| H2O | ж | 69,94 | NO | г | 210,20 |
| Fе2О3 | к | 89,96 | CO2 | г | 213,65 |
| NH4C1 | к | 94,5 | C2H4 | г | 219,45 |
| СН3ОН | ж | 126,8 | Cl2 | г | 222,95 |
| Н2 | г | 130,59 | NO2 | г | 240,46 |
| Fе3O4 | к | 146,4 | РС13 | г | 311,66 |
| СН4 | г | 186,19 | PCl5 | г | 352,71 |
| НС1 | г | 186,68 |
Пример 3. На основании стандартных теплот образования (см. табл. 15) и абсолютных стандартных энтропий веществ (табл.17) вычислите 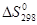 реакции, протекающей по уравнению
реакции, протекающей по уравнению
СО(г)+Н2О(ж)=СО2(г)+Н2(г)
Решение.  G0 =
G0 =  H0 - T
H0 - T  S0;
S0;  H и
H и  S – функции состояния, поэтому
S – функции состояния, поэтому
∆Н0х.р.=∑ ∆Н0прод - ∑ ∆Н0исх ; ∆S0x.p.= ∑S0прод - ∑ S0 исх
∆Н0х.р.=(-393,51+0) – (110,52 – 285,84) = +2,85 кДж
∆S0x.p.=(213,65+130,59)-(197,91+69,94) = +76,39 = 0,07639 кДж/(моль∙К);
∆G0= +2,85 – 298 ∙ 0,07639 = - 19,91 кДж
Пример 4. Реакция восстановления Fе2О3 водородом протекает по уравнению
Fe2O3(к)+3H2(г) = 2Fe(к)+3H2O(г); ∆Н=+96,61 кДж
Возможна ли эта реакция при стандартных условиях, если изменение энтропии  S=0,1387 кДж/(моль×К)? При какой температуре начнется восстановление Fе2О3?
S=0,1387 кДж/(моль×К)? При какой температуре начнется восстановление Fе2О3?
Решение. Вычисляем  G0 реакции:
G0 реакции:
∆G = ∆Н-Т∆S = 96,61 – 298 ∙ 0,1387 = +55,28 кДж
Так как  G > 0, то реакция при стандартных условиях невозможна; наоборот, при этих условиях идет обратная реакция окисления железа (коррозия). Найдем температуру, при которой
G > 0, то реакция при стандартных условиях невозможна; наоборот, при этих условиях идет обратная реакция окисления железа (коррозия). Найдем температуру, при которой  G=0:
G=0:
∆Н 96,61

 ∆Н =Т∆S; Т = = = 696,5 К
∆Н =Т∆S; Т = = = 696,5 К
∆S 0,1387
Следовательно, при температуре»696,5 К начнется реакция восстановления Fе2О3 Иногда эту температуру называют температурой начала реакции.
Пример 5. Вычислите  H0,
H0,  S и
S и  G0 реакции, протекающей по уравнению
G0 реакции, протекающей по уравнению
Fe2O3(к) + 3C = 2Fe + 3CO
Возможна ли реакция восстановления Fе2О3 углеродом при 500 и 1000 К?
Решение.  H0xp и
H0xp и  S0xp находим из соотношений (1) и (2) (см. разделы «Энергетика химических процессов. Термохимические расчеты» и «Химическое сродство»):
S0xp находим из соотношений (1) и (2) (см. разделы «Энергетика химических процессов. Термохимические расчеты» и «Химическое сродство»):
∆Н0x.p.= [3(-110,52)+2 ∙ 0] – [- 822,10 + 3 ∙ 0] = -331,56+822,10 = +490,54 кДж
∆S0x.p.=(2 ∙ 27,2+3 ∙ 197,91) – (89,96+3 ∙ 5,69) = 541,1 Дж/(моль ∙ К)
Энергию Гиббса при соответствующих температурах находим из соотношения
541,1
 ∆G500 = 490,54 – 500 = 219,99 кДж
∆G500 = 490,54 – 500 = 219,99 кДж
541,1
 ∆G1000 = 490,54 – 1000 = 50,56 кДж
∆G1000 = 490,54 – 1000 = 50,56 кДж
Так как  G500>0, a
G500>0, a  G1000<0, то восстановление Fе2О3 возможно при 1000 К и невозможно при 500 К.
G1000<0, то восстановление Fе2О3 возможно при 1000 К и невозможно при 500 К.
Поиск по сайту: