Елементи теорії відсотків

В процесі нарощування і дисконтування грошей розглядаються наступні чотири взаємопов'язані чинники:

1) сучасне значення грошей (PV)

2) майбутнє значення грошей (FV)

3) час, виражений в днях t або кількості періодів n

4) норма прибутковості (процентна ставка).

Характер взаємовідношення між ними визначається способом нарахування прибутковості, або частіше говорять – відсотків.

Розрізняють дві схеми нарахування відсотків: прості відсотки і складні відсотки.

Прості відсотки. У схемі простих відсотків нарахування доходу на інвестовану суму грошей здійснюється завжди виходячи з початкової суми інвестицій.

Інвестор розмістив на депозитному рахунку 1,000 грн. при процентній ставці 40 простих річних відсотків. У випадку, якщо він не зніматиме грошей з свого рахунку, через рік він матиме FV = 1,000 + 400 = 1,400 грн.

А через два роки FV = 1,000 + 400 + 400 = 1,800 грн.

Таким чином, загальна формула нарахування простих відсотків має наступний вигляд . (3)

У формулі (3) nможе мати дробове значення, коли йдеться про частину періоду (роки).

Дисконтування при простих відсотках здійснюється за допомогою формули, яка виходить шляхом звернення (3): (4)

Приклад. Ви збирається накопичити 50,000 грн. протягом року за допомогою банківського депозиту, який пропонує щомісячне нарахування простих відсотків по місячній процентній ставці 5%. Яку суму необхідно покласти на депозит? З формули (4) виходить .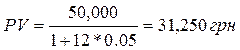

Складні відсотки. Складним відсоткомназивається сума доходу, яка утворюється в результаті інвестування грошей за умови, що сума нарахованого простого відсотка не виплачується в кінці кожного періоду, а приєднується до суми основного внеску і в наступному платіжному періоді сама приносить дохід.

При нормі прибутковості r маємо:

· у перший рік: ,

· у другий рік: і т.д.

Таким чином, загальна формула для нарахування складних відсотків має наступний вигляд: 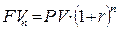(7)

Справжнє (сучасне) значення вартості певної майбутньої суми грошей обчислюється за допомогою формули: . (8)

Розглянемо співвідношення між показниками нарощування для простих і складних відсотків. За допомогою простих міркувань алгебри неважко встановити

· якщо n < 1 року, то 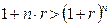. Інвестувати при простих відсотках вигідніше

· якщо n > 1 року, то . Більш вигідним для інвестора є схема складних відсотків.

· якщо n = 1 рік, то . В цьому випадку вибір варіанту значення не має.

Нехай відсотки нараховуються m раз на рік, тоді процентна ставка в перерахунку на період буде рівна r/m, а кількість періодів буде дорівнювати nm. Відповідно до початкової формули (7) в цьому випадку нарощування проводитиметься за допомогою наступного співвідношення:

. (9)

Формула для обчислення справжньої вартості також приймає наступний узагальнений вигляд:

. (10)

Приклад. Що вигідніше при вкладенні грошей на 2 роки: процентна ставка 40% річних при нарахуванні відсотків 2 рази на рік, або ставка 38% річних, таких, що нараховуються 12 разів на рік?

Розрахуємо показник нарощування за допомогою формули (9):

,

.

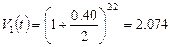Очевидно, що другий варіант більш вигідний.

Поиск по сайту: