Реалізація логічних функцій у поширених базисах

В. Кофанов

ПРОЕКТУВАННЯ

ЦИФРОВИХ ПРИСТРОЇВ

b a b a

&

Міністерство освіти і науки України

Вінницький національний технічний університет

Кафедра радіотехніки

В. Кофанов

ПРОЕКТУВАННЯ

ЦИФРОВИХ ПРИСТРОЇВ

Навчальний посібник для курсового проектування

з дисципліни „Цифрові пристрої та мікропроцесори, ч. І”

ПРОЕКТУВАННЯ НА МІС

Реалізація логічних функцій у поширених базисах

Під час проектування ЦП на сучасній елементній базі – програмованих ВІС/НВІС – програмні модулі компілятора САПР оптимізують схему, виходячи із заданих вимог швидкодії, потрібного ресурсу мікросхеми і т. ін. З огляду на це втрачають великого значення питання мінімізації і перетворення схем до певного базису вручну. Проте подібні перетворення мають сенс із точки зору розуміння цифрової схемотехніки і введення проектів у канонічному та наочному вигляді. Проектування на старій елементній базі (на ІС жорсткої структури) допоміжних кіл і поготів цілого пристрою потребує перетворювати схеми або їх фрагменти від одного базису до іншого. Мета таких перетворень – вкорочення схем, використання вільних логічних елементів усередині корпусів частково задіяних мікросхем, зменшення кількості їх типономіналів (що є важливо в потоковому виробництві), а також використання основних і, часто, кращих за параметрами логічних елементів певної серії ІС. Розглянемо перетворення до найпоширеніших базисів.

1 Базис І-НЕ. Реалізація найпростіших елементів у базисі І-НЕ випливає безпосередньо зі співвідношень алгебри логіки [1]. Наприклад, легко довести самостійно еквівалентність елементів НЕ, І, АБО, АБО-НЕ, І-АБО-НЕ на рис. 1.1, а... ґ.

Реалізацію складніших функцій в базисі І-НЕ звичайно виконують алгебрично, за формулою:

(1.1)

де А, В – кон’юнкції літералів (змінних або їх заперечень). Тобто для такого перетворення необхідно:

а) мінімізувати функцію в МДНФ (об’єднанням одиниць) або, якщо не підлягає мінімізації, записати в ДДНФ;

б) поставити над виразом два знаки інверсії та за законом двоїстості перейти від суми до добутку змінних або їх кон’юнкцій.

Приклад 1. Для функцій Виключне АБО та Виключне АБО-НЕ перетворюємо за виразом (1.1) структурні функції

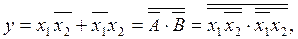
і реалізуємо схеми на елементах І-НЕ (рис. 1.1, д,е).

2 Базис АБО-НЕ. Реалізація логічних елементів НЕ, АБО, І, І-НЕ, АБО-І-НЕ (рис. 1.2, а... ґ) у базисі АБО-НЕ повністю дуальні перетворенням у базисі І-НЕ.

Алгебрично для переходу до базису АБО-НЕ перетворення виконують за формулою:

, (1.2)

(тут А, В – диз’юнкції літералів), тобто в такому порядку:

а) мінімізують функцію в МКНФ (об’єднанням нулів) або, якщо не підлягає мінімізації, записують у ДКНФ;

б) позначають над виразом два знаки інверсії та переходять від добутку до логічного додавання за законом двоїстості.

Приклад 2. Для функцій Виключне АБО та Виключне АБО-НЕ перетворюємо за виразом (1.2) структурні функції

,

і реалізуємо схеми на елементах АБО-НЕ (рис. 1.2, д,е).

3 Базис І-АБО-НЕ. Перетворенням за законами двоїстості, наприклад, функції АБО-І

можна дістати її реалізацію в базисі І-АБО-НЕ (рис. 1.3, а). Перетворення схем, взагалі, виконують алгебрично за формулами

, (1.3)

тобто в послідовності:

а) мінімізують інверсну функцію в МДНФ (об’єднанням нулів);

б) за допомогою інверсії над обома частинами виразу переходять до структурної функції в базисі І-АБО-НЕ.

Приклад 3. Для функції Виключне АБО перетворюємо за виразом (1.3) структурну функцію

,

зручну для побудови в базисі І-АБО-НЕ (рис. 1.3, б).

Поиск по сайту: