Способи спрощення логічних схем

Після мінімізації логічної функції в булевому базисі доцільно ще перетворити її до структурної форми таким чином, аби схема потребувала мінімуму логічних елементів, а часто ще й мінімуму виводів. Проте проблема схемної мінімізації в різних функціонально повних системах в загальному вигляді на цей час не розв'язана.

Аби полегшити подібні перетворення, розглянемо окремі прийоми схемної мінімізації, тобто способи зменшення складності логічної схеми. Як показник її складності зазвичай використовується потрібна кількість корпусів q _к однотипних ІС. На стадії логічного проектування відносно простих схем користуються показником складності структурної функції у вигляді суми q = q _е + q _в потрібної кількості логічних елементів q _е та загальної кількості їх входів q _в (іноді складність зручніше оцінювати потрібною загальною кількістю зовнішніх виводів інтегрованих мікросхем q _з.в). Проте наочним для порівняння схем і зручним під час їх технічної реалізації на логічних елементах (на вентильному рівні) є показник у вигляді зазначення через риску кількості елементів на загальну кількість їх входів q = q _е / q _в, яким і користуватимемося далі.

Складність легко оцінити безпосередньо з виразу підрахуванням кількості логічних операцій та змінних (літер), що входять до кожної з них. Так, для реалізації елементів Виключне АБО та Виключне АБО-НЕ потребується три двовходові елементи та два інвертори по одному входу, тобто разом q = 5/8 (див. рис. 1.1, д,е, 1.2, д,е). У виразах, перетворених до базисів І-НЕ та АБО-НЕ, досить підрахувати кількість знаків інверсії (елементи) та змінних під кожним з них (входи).

1 Редукція в диз'юнктивній формі. Якщо об'єднанню до сполук з більшої кількості одиниць на діаграмі термів заважають окремі нулі, функцію можна спростити, розглядаючи спочатку ці нулі як одиниці, а відтак скоригувати її вилученням з множини одиниць зайві нульові клітинки. Систематизовану процедуру такого спрощення називають редукцією. У загальному вигляді під час мінімізації в ДНФ редукцію можна виконати доповненням заданої функції у неперетинною з нею допоміжною функцією у ₁ таким чином, аби об'єднання D цих функцій та сама допоміжна функція у ₁були якомога простішими. Використовуючи операцію заборони для вилучення зайвих клітинок, шукану функцію дістаємо з виразу

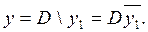(1.4)

Приклад 1. Мінімізацією звичайним чином функції, заданій діаграмою 1 (множина одиниць) на рис. 1.4, а

маємо реалізацію її в базисі І-НЕ складністю q =7/13. Редукцію виконуємо в такий спосіб. Введенням допоміжної функції y ₁ = x ₁ x ₂(зазначена зірочками) мінімізуємо утворене об'єднання (на діаграмі обведено)

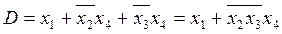
і за (1.4) у підсумку отримуємо структурну функцію

яка реалізується мінімальною схемою в базисі І-НЕ складністю q =5/11 (рис. 1.4, б).

З метою спрощення допоміжної функції до неї можна долучити інші нульові клітинки (якщо вони є), які не входять до об'єднання. При цьому корекція за виразом (1.4) не змінює функцію, бо згідно з операцією заборони 0 \ 1 = 0.

Приклад 2. Якщо в нашому прикладі утворити об'єднання, обведене на діаграмі (2) D = x 1 + x 4, то для вилучення зайвих клітинок, позначених зірочками, до допоміжної функції (пунктир) додаємо ще шосту клітинку: y 1 = x 1 x 2 + x 2 x 3. У підсумку маємо шукану функцію

яка реалізується мінімальною схемою з використанням елемента І-АБО-НЕ складністю q =4/10 (рис. 1.4, в).

Цілком зрозуміло, що редукцію можна застосувати і не до функції в цілому, а лише до її фрагменту, якщо така процедура приводить до мінімальнішої форми. Тоді, під час коригування фрагменту за (1.4) до допоміжної функції з метою її спрощення можна долучити одиничні клітинки, що перетинаються з рештою функції. Це означає, що мінтерм, охоплений однією сполукою одиниць, не обов'язково повторювати в інших сполуках.

Приклад 3. На діаграмі (3) частину функції (верхня половина діаграми) не має потреби коригувати, а з решти одиниць та нульової клітинки, поміченої зірочкою, утворюємо об'єднання D = x 1 + x 3(обведено суцільною лінією). Для вилучення нульової клітинки до допоміжної функції y 1 = x 1 x 2 x 3додаємо ще сьому клітинку, бо вона вже репрезентована у функції частиною . Отже, маємо структурну функцію

для реалізації в базисі І-НЕ за мінімальною схемою (рис. 1.4, г) складністю q = 4/10 (проти 7/13 або 6/12 у варіантах без редукції).

2 Редукція в кон'юнктивній формі. Враховуючи дуальність алгебри логіки щодо логічних функцій І та АБО, аналогічну редукцію можна виконати і під час мінімізації в КНФ. Але тепер до нульових клітинок функції у з метою спрощення їх сполук на діаграмі долучаємо ще деякі одиничні клітинки, утворюючи допоміжну функцію у 1, якщо доповнення об'єднання цих функцій (тобто сполучення нульових і ще приєднаних одиничних клітинок) і нова функція у 1виявляються простими. Для здобуття шуканої функції необхідно в утвореному об'єднанні відновити одиничні клітинки, тобто виконати операцію імплікації

(1.5)

Приклад 4. Так, МКНФ функції, що задана діаграмою (4) на рис. 1.4, а, перетворена до базису АБО-НЕ, відповідає складності q =7/13:

Для редукції спочатку з одиничних клітинок (помічені зірочками) утворюємо допоміжну функцію, яку (вважаючи ці клітинки нульовими) зображаємо в МКНФ: у 1 = х 1 + х 2. Відтак долученням цих клітинок до нульових утворюємо доповнення об'єднання (обведено суцільною лінією) і також мінімізуємо його в МКНФ:

Нарешті, за (1.5) дістаємо спрощений вираз шуканої функції

та користуючись розподільчим законом ab + c = (a + c)(b + c) переходимо до базису АБО-НЕ

зі складністю q = 5/11 (відповідає схемі на рис. 1.4, б, якщо елементи І-НЕ замінити на АБО-НЕ).

3 Алгебричне виконання редукції. Наведена в п. 1, 2 графічна процедура редукції за допомогою діаграм термів є наочною і практично не потребує тотожних перетворень. Природно, у простих випадках редукцію можна виконати і аналітично.

Алгебрично редукцію виконувати доцільно у випадку різного входження однакових змінних (без інверсії та з інверсією) до кількох термів безпосередньо за формулами в диз'юнктивній та кон'юнктивній формах відповідно:

(1.6)

(1.7)

Приклад 5. Застосовуючи двічі перетворення за (1.6, 1.7) до виразів функцій Виключне АБО та Виключне АБО-НЕ

дістанемо мінімальні схеми реалізації цих елементів відповідно в базисах І-НЕ та АБО-НЕ складністю 4/8 (на рис. 1.4, ґ наведено одну з двох цих дуальних схем).

Узагальнюючи, можна дійти висновку, що процедура редукції відображається на схемі додатковим рівнем сполучення логічних елементів. З утворених спрощених сполук діаграми зайві клітинки (разом з приєднаними, за змогою, сусідніми) вилучаються за допомогою тих логічних елементів вхідного рівня, виходи яких є спільними для входів кількох елементів наступного схемного рівня. Це добре видно з наведених прикладів на рис. 1.4, б,в,г, ґ.

4 Реалізація в мішаній формі. Для введення проектів на сучасних ВІС програмованої структури форма зображення функції не має істотного значення, а розвинути серії інтегрованих мікросхем жорсткої структури містять широку номенклатуру типономіналів. З огляду на це для спрощення схем широко використовують різні логічні елементи, тобто практично структурну функцію часто реалізують у мішаній формі. Передусім, спрощення виконують зменшенням кількості інверсій, зокрема, без переходу до іншого базису.

Приклад 6. Формули виразів, наприклад, для функції Виключне АБО перетворюють у вигляді

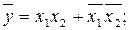
і реалізують без додаткових інверторів як для прикладу на рис. 1.4, д подано схему для другої з цих мінімальних форм.

У мішаній формі з використанням складніших елементів, що виконують різноманітні логічні функції, можна значно спростити схему. Прикладами є вже розглянута реалізація з використанням елементів І-АБО-НЕ (див. рис. 1.3, б), а також виокремлення елемента Виключне АБО, наведене в п. 5.

5 Каскадна реалізація термів. Сутність такого спрощення полягає в тому, що в первісному по мінімізації виразі відокремлюють спільні для кількох термів частини винесенням їх за дужки, позначають якимось символом і використовують кілька разів для реалізації функції, внаслідок чого схема в цілому вкорочується.

Приклад 7. Розглянемо такий прийом на прикладі функції, заданій таблицею термів на рис. 1.4, е. За сполуками одиниць дістаємо МДНФ

,

що реалізується схемою, фрагмент якої наведено на рис. 1.4, є, складністю q = 9/20 з урахуванням вхідних інверторів, які тут і далі не показані. Спрощення виконуємо таким чином. Позначаємо спільні частини , , виносимо їх за дужки та перетворюємо МДНФ з урахуванням (1.6)

Отже, складність схеми зменшується до q = 7/12 (рис. 1.4, ж). Якщо доповнити сполуки одиниць долученням дев'ятої клітинки, цього ж висліду можна дійти коротше, процедурою редукції.

Ще більше спрощується схема відокремленням елемента Виключне АБО

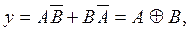
складність її становить q = 5/8 (рис. 1.4, з).

6 Частково визначені функції. Якщо деякі вхідні кортежі за умов роботи пристрою не виникають, то функція є частково визначеною. Наприклад, у двійково-десяткових кодах набори змінних при Х ₁₀ > 9 є заборонені, тобто функція на цих наборах лишається невизначеною, що можна тлумачити як байдужі (факультативні) її значення X = 0 або 1, бо вони не зустрічаються під час правильної роботи пристрою.

Приклад 8. Хай функція чотирьох змінних набуває одиничного значення на кортежах: i =0, 1, 2, 12, 13, 14, крім того, забороненими є кортежі i =3, 7, 11, 15 та нульовими всі інші. На діаграмі термів (рис. 1.4, и) факультативні значення функції помічено позначкою Х. З метою спрощення під час мінімізації функції невизначені умови довизначають таким чином, аби утворювались найбільші сполуки з одиниць, а далі мінімізують як звичайно. У прикладі в двох клітинках, які доцільно приєднати до одиниць, вважаємо X=1, а в двох інших – X=0. Зчитування по утворенні сполук дає спрощену МДНФ

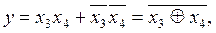
що є функцією Виключне АБО-НЕ. Не важко переконатись, що той самий результат отримаємо об’єднанням на діаграмі нулів і аналогічним довизначенням клітинок X.

Отже, чим більше існує заборонених кортежів, на яких функція є невизначеною, тим більше є можливості для її спрощення.

Таким чином, після мінімізації логічну функцію доцільно додатково спростити для реалізації її з урахуванням потрібного елементного базису. Для цього застосовують перетворення по зменшенню кількості інверсій в термах, переходу до структурної функції в мішаній формі, відокремленню спільних фрагментів у кількох термах з метою їх каскадної реалізації, використанню складніших елементів, зокрема, типових пристроїв більшого ступеня інтеграції.

Поиск по сайту: