 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Проработка структуры вопросов для каждого класса запросов
Процесс трансляции вопроса к модели представляет собой синхронизацию вопроса на естественном языке с соответствующим шаблоном запроса на языке модели (как показано на рисунке 4.1).

Рисунок 4.1 – Процесс трансляции вопроса к модели
То есть весь процесс трансляции состоит из двух этапов:
1) Вопрос пользователя, заданный на естественном языке анализируется на наличие типовых объектов и характер взаимосвязей между ними. В результате чего определяется тип запроса к модели, который необходимо использовать.
2) Затем запрос выражается на языке модели, понятном генератору отчетов, для дальнейшего формирования ответа на запрос.
Таблица 4.1 – Примеры вопросов для каждого класса запросов, относящиеся к процессу «Создать, поддерживать и совершенствовать систему производства ресиверов»
| Класс запроса | Форма вопроса | Объект вопроса | Пример | Запрос |
| В условиях определенности | Имеются ли… | Процессы | Имеются ли процессы СП ресиверов, по которым отсутствуют записи? | |
| Документы | Имеются ли записи операции «Рубить прутки» процесса «Произвести партию ресиверов»? | |||
| Кто является в организации … процесса… | представителем руководства по качеству | Кто является в организации представителем руководства по качеству? | ||
| ответственным исполнителем | Кто является ответственным исполнителем процесса «Штамповать заготовки»? | |||
| Определены ли…, необходимые для результативного функционирования | процессы | Определены ли процессы, необходимые для результативного функционирования СП ресиверов? | ||
| ресурсы | Определены ли ресурсы, необходимые для результативного функционирования СП ресиверов? |
| Окончание таблицы 4.1 | ||||
| критерии и методы | Определены ли критерии результативности на этапах производства партии ресиверов? | |||
| В условиях частичной неопределенности | Подтверждается ли наличие в организации… | СМК | Подтверждается ли наличие в организации СМК? | |
| Находятся ли в управляемых условиях… | документы | Находятся ли в управляемых условиях документированные процедуры процесса «Создать, поддерживать и совершенствовать систему производства ресиверов»? | ||
| процессы | Находятся ли в управляемых условиях процесс «Осуществлять менеджмент персонала» СП ресиверов? | |||
| ресурсы | Находятся ли в управляемых условиях ресурсы организации? | |||
| Проводится ли … | процесс | Проходится ли верификация деталей на этапе процесса «Собрать и сварить детали в ресивер»? | ||
| Поддерживается ли … в рабочем состоянии | СМК | Поддерживается ли СМК в рабочем состоянии? | ||
| документ | Поддерживается ли РК СП ресиверов в рабочем состоянии? | |||
| В условиях полной неопределенности | Какова причина … | Какова причина дефекта ресивера на этапе процесса «Собрать и сварить детали в ресивер»? |
Практическое применение ЭС в организации как источника знаний представлено на рисунке 4.2.
Запросы

Рисунок 4.2 – Практическое применение ЭС в организации как источника знаний
Самой большой проблемой и главной задаче перед владельцем экспертной системы деятельности организации будет научить систему отвечать на вопросы в условиях полной неопределенности.
В рамках дипломного проекта была разработана методология формирования таких запросов при помощи планирования эксперимента.
(Рисунок 4.3).
 Рисунок 4.3 – Первый этап планирования эксперимента
Рисунок 4.3 – Первый этап планирования эксперимента
Эксперимент состоит из двух этапов:
1. Полнофакторный эксперимент по оценке значимости факторов на качество продукции – отвечает на вопросы:
«Какие факторы являются потенциальными причинами дефекта или несоответствия и в какой степени?»
«Являются ли влияющие факторы независимыми, а если зависимыми, то как и в какой мере?»
2. Оценка вероятности того, что причиной появления дефекта является тот или иной фактор – отвечает на вопросы:
«Какова вероятность того, что появления дефекта (несоответствия) вызвано тем или иным фактором?»
На качество продукции в общем случае оказывают влияние следующие комплексные факторы:
- ресурс типа «Механизм»:
- персонал;
- инфраструктура;
- производственная среда;
- ресурс типа «Управление»
- документация СП
- внешняя документация (СТБ, ГОСТ, ТР)
- внутренняя документация (ТИ, ТР, ОРД);
- ресурс типа «Вход»:
- материалы и комплектующие;
- заявка и требования потребителя.
Обобщенную модель зависимости можно представить следующим образом

где  – качество ресиверов;
– качество ресиверов;
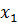 – комплексный ресурс типа «Механизм»;
– комплексный ресурс типа «Механизм»;
 – комплексный ресурс типа «Управление»;
– комплексный ресурс типа «Управление»;
 – комплексный ресурс типа «Вход».
– комплексный ресурс типа «Вход».
Факторы могут принимать, следующие значения: 0 – ресурс, не соответствующий требованиям; 1 – ресурс, соответствующий требованиям.
Весь эксперимент проходит в несколько этапов.
Этап 1
Цели:
- оценка влияния факторов «Механизм», «Управление», «Вход» на качество продукции;
- оценка независимости (взаимного влияния) факторов.
Для оценки значимости каждого фактора на качество ресивера необходимо провести ПФЭ методом попарного альтернативного сопоставления. Для оценивания применим шкалу сравнительного превосходства, представленную в таблице 4.3.
Таблица 4.3 – Шкала сравнительного превосходства
| Ранг | Определение | Балл |
| A | Одинаковый уровень значимости | 0 |
| B | Почти эквивалентный уровень значимости | 1 |
| C | Несколько предпочтительней уровень значимости | 3 |
| D | Значительно предпочтительней уровень значимости | 5 |
| E | Строго предпочтительней уровень значимости | 7 |
| F | Строго предпочтительней уровень значимости | 8 |
| 2,4,6 | Промежуточные значения между двумя соседними рангами |
Для построения модели эксперимента используется метод покоординатного спуска, поскольку точек эксперимента восемь, а метод оценивания – попарное альтернативное сопоставление. Получается 3 итерации проведения эксперимента, как показано на рисунке 4.4 и
таблице 4.4.

Рисунок 4.4 – Метод покоординатного спуска
Таблица 4.4 – Схема проведения эксперимента по итерациям
| Итерация 1 | Итерация 2 | Итерация 3 |

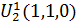


| 



| 



|
Далее по каждой итерации проводится оценивание с привлечением эксперта методом попарного альтернативного сопоставления (таблицы 4.5-4.6).
Таблица 4.5 – Итерация 1
| План A1 | План B1 | |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||
Принимаем 
| ||||

| 
| |||
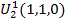
| 0,833 | 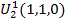
| 0,286 | |

| 0,500 | 
| 0,286 | |

| 
| |||
Таблица 4.6 – Итерация 2
| План A2 | План B2 | ||
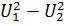
| 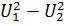
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||
Принимаем 
| |||

| 
| ||

| 0,769 | 
| 0,429 |

| 0,462 | 
| 0,286 |

| 
|
Таблица 4.7 – Итерация 3
| План A3 | План B3 | |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||

| 
| |||
Принимаем 
| ||||

| 
| |||
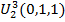
| 0,750 | 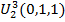
| 0,571 | |

| 0,438 | 
| 0,429 | |

| 
| |||
Нормализованные данные по каждой ситуации сведем в общую таблицу 4.8.
Таблица 4.8 – Нормализованные данные по итерациям
| План А | План В | ||

| 
| ||
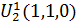
| 0,833 | 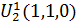
| 0,857 |

| 0,500 | 
| 0,286 |

| 0,769 | 
| 0,429 |

| 0,462 | 
| 0,286 |

| 0,750 | 
| 0,571 |

| 0,438 | 
| 0,429 |

| 
|
Обработав данные эксперимента, необходимо проверить устойчивость результатов экспертного эксперимента по критерию К1.
Критерий К1: Считаем, что результаты экспертного оценивания устойчивы, если данные связаны линейной возрастающей значимой зависимостью,, т.е. справедлива следующая зависимость:

где  – результат эксперимента по плану А и по плану В соответственно;
– результат эксперимента по плану А и по плану В соответственно;
 – линейный коэффициент;
– линейный коэффициент;
 – свободный коэффициент.
– свободный коэффициент.
Выдвигается гипотеза H0, которая сформулирована следующим образом: коэффициент линейного уравнения равен 0:  .
.
Если вероятность p<0,2, то гипотеза отвергается.
Задачу линейной линейной регрессии решаем с помощью пакета Statistica (рисунок 4.5).

Рисунок 4.5 – График линейной зависимости планов экспериментов
Полнофакторный эксперимент предполагает следующую математическую модель
 ,
,
где  – линейные эффекты (коэффициенты);
– линейные эффекты (коэффициенты);
 – эффекты (коэффициенты) парного взаимодействия;
– эффекты (коэффициенты) парного взаимодействия;
 – эффект (коэффициенты) тройного взаимодействия.
– эффект (коэффициенты) тройного взаимодействия.
Необходима проверить модель эксперимента на значимость. Для этого принимаем гипотезу H0, которая звучит следующим образом: коэффициент линейных, парных или тройных взаимодействий равны нулю. Для проверки гипотезы необходимо определить уровень значимости p-level: p=0,05. Если p>0,05 – гипотеза принимается. Если p<0,05 – гипотеза отвергается.
Гипотеза H0 проверяется с помощью пакета Statistica.
1. Проверяется значимость линейных взаимодействий
(рисунки 4.6).

Рисунок 4.6 – Проверка значимости линейных взаимодействий
Результаты оценивания значений факторов эксперимента представлены на рисунке 4.7.

Рисунок 4.7 – Значения факторов эксперимента
В появившемся окне:
R – коэффициент корреляции;
B – коэффициент уравнения регрессии;
R2 – коэффициент детерминации.
p-level(X1), p-level(X2), p-level(X3)<0,05, следовательно гипотезу H0 можно отвергнуть, т.е.  .
.
 =0,333,
=0,333,  = 0,373,
= 0,373,  =0,270.
=0,270.
2. После этого проводится проверка на значимость парных взаимодействий факторов эксперимента (рисунки 4.8).

Рисунок 4.8 – Значения парных взаимодействий факторов эксперимента
Результаты проверки значимости парного взаимодействия факторов «Механизм» и «Управление» представлены на рисунке 4.9.

Рисунок 4.9 – Результаты проверки значимости парного взаимодействия факторов «Механизм» и «Управление»
Результаты проверки значимости парного взаимодействия факторов «Управление» и «Вход» представлены на рисунке 4.10.

Рисунок 4.10 – Результаты проверки значимости парного взаимодействия факторов «Управление» и «Вход»
Результаты проверки значимости парного взаимодействия факторов «Механизм» и «Вход» представлены на рисунке 4.11.

Рисунок 4.11 – Результаты проверки значимости парного взаимодействия факторов «Механизмы» и «Вход»
В появившихся окнах:
R – коэффициент корреляции;
B – коэффициент уравнения регрессии;
R2 – коэффициент детерминации.
p-level(X1X2), p-level(X3X2), p-level(X1X3)>0,05, следовательно
гипотезу H0 можно принять, т.е.  .
.
3. Проверяется значимость тройного взаимодействия факторов (рисунки 4.12).

Рисунок 4.12 –Значения тройного взаимодействия факторов эксперимента
Результаты проверки значимости тройного взаимодействия факторов «Механизм», «Управление» и «Вход» представлены на рисунке 4.13.

Рисунок 4.13 – Результаты проверки значимости тройного взаимодействия факторов «Механизм», «Управление» и «Вход»
В появившемся окне:
R – коэффициент корреляции;
B – коэффициент уравнения регрессии;
R2 – коэффициент детерминации.
p-level(X1X2X3),>0,05, следовательно гипотезу H0 можно принять, т.е.  .
.
4. Проведя оценку влияния факторов на качество продукции, можно записать модель ПФЭ в виде уравнения регрессии:
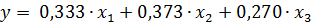
РЕЗЮМЕ: По результатам полнофакторного эксперимента и построенной модели можно сделать вывод о том, что выделенные факторы «Механизм», «Управление», «Вход» приблизительно в равной мере оказывают влияние на качество продукции. Но при этом полученное уравнение регрессии, что действие одновременно двух или трех факторов не оказывает существенного влияния на качество продукции и при проведении дальнейшего исследования не требуется рассмотрение таких взаимодействий.
Этап 2
Цель:
- оценка вероятности того, что причиной появления дефекта является тот или иной фактор;
- определение первоочередного пути поиска причины дефекта.
Для оценки вероятностей применим методом попарного альтернативного сопоставления. Для оценивания применяется шкала сравнительного превосходства, представленной в таблице 4.9.
Таблица 4.9 – Шкала сравнительного превосходства
| Ранг | Определение | Балл |
| A | Одинаковый уровень значимости | 0 |
| B | Почти эквивалентный уровень значимости | 1 |
| C | Несколько предпочтительней уровень значимости | 3 |
| D | Значительно предпочтительней уровень значимости | 5 |
| E | Строго предпочтительней уровень значимости | 7 |
| F | Строго предпочтительней уровень значимости | 8 |
| 2,4,6 | Промежуточные значения между двумя соседними рангами |
Рассматриваются одна крайняя ситуации, когда все факторы принимают наилучшие значения, и промежуточные ситуации, когда один из факторов принимает наихудшее значение (0), а остальные – максимальные значения (1).
Возможные ситуации рассмотрены в таблице 4.10.
Таблица 4.10 – Возможные ситуации
| Математическое выражение ситуации | Пояснение |

| Причина дефекта – ресурс «Механизм» при условии, что ресурсы «Управление» и «Вход» соответствуют требованиям |

| Причина дефекта – ресурс «Управление» при условии, что ресурсы «Механизм» и «Вход» соответствуют требованиям |

| Причина дефекта – ресурс «Вход» при условии, что ресурсы «Механизм» и «Управление» соответствуют требованиям |

| Ситуация при условии, ресурсы «Механизм», «Управление» и «Вход» соответствуют требованиям |
Далее оценивание с привлечением эксперта методом попарного альтернативного сопоставления (Таблица 4.11).
Таблица 4.11 – Результаты экспертного оценивания
| План A | План B | ||||

| 
| - | |||

| 
| - | |||

| 
| - | |||
| U4 | U4 | - | |||
| U3 | U3 | - | |||
| U2 | U2 | - | |||
| U1 | U1 | - | |||
Принимаем 
| 
| ||||
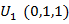
| 
| ||||

| 0,785 | 
| 0,714 | 0,7495 | |

| 0,500 | 
| 0,286 | 0,393 | |

| 
| ||||
Обработав данные эксперимента, необходимо проверить устойчивость результатов экспертного эксперимента по критерию К1.
Критерий К1: Считаем, что результаты экспертного оценивания устойчивы, если данные связаны линейной возрастающей значимой зависимостью.
Задачу линейной линейной регрессии решаем с помощью пакета Statistica, которая заключается в проверке того, что коэффициент k является значимым в уравнении:

где  – значение величины по плану А и по плану В соответственно;
– значение величины по плану А и по плану В соответственно;
 – линейный коэффициент;
– линейный коэффициент;
 – свободный коэффициент.
– свободный коэффициент.
Выдвигается гипотеза H0, которая звучит следующим образом: коэффициент  . Для проверки гипотезы необходимо определить уровень значимости p-level: p=0,05. Если p>0,05 – гипотеза принимается. Если p<0,05 – гипотеза отвергается (рисунки 4.14-4.15).
. Для проверки гипотезы необходимо определить уровень значимости p-level: p=0,05. Если p>0,05 – гипотеза принимается. Если p<0,05 – гипотеза отвергается (рисунки 4.14-4.15).

Рисунок 4.14– Таблица значений факторов по плану А и В

Рисунок 4.15 – Проверка значимости коэффициента линейной регрессии
В появившемся окне:
R – коэффициент корреляции;
B – коэффициент уравнения регрессии;
R2 – коэффициент детерминации.
p-level( )=0,026<0,05, следовательно гипотезу H0 можно отвергнуть, т.е.
)=0,026<0,05, следовательно гипотезу H0 можно отвергнуть, т.е.  :
:
Строится график зависимости результатов по Плану А и по плану В (рисунок 4.16) и рассчитывается.

Рисунок 4.16 – График линейной зависимости планов экспериментов
РЕЗЮМЕ: Из полученных результатов можно сделать вывод о том, что наиболее вероятной причиной дефекта ресивера является ресурс типа «Механизм» – 1. Следовательно, первоочередным путем поиска причины – дефекта являются ресурсы:
- персонал;
- инфраструктура;
- производственная среда.
Поскольку выделенные факторы являются комплексными, существует необходимость их декомпозиции. В случае проведенного эксперимента декомпозиции подлежит ресурс «Механизм». Для дальнейшего определения пути поиска причины дефекта необходимо повторить эксперимент при влиянии таких факторов, как персонал, инфраструктура и производственная среда (рисунок 4.17).

Рисунок 4.17 – Декомпозиция ресурса «Механизм»
Как известно, каждый ресурс процесса является результатом деятельности (выходом) другого процесса, который, в свою очередь имеет свои ресурсы на входе, как показано на рисунке 4.18.

Рисунок 4.18 – Реализация системно-комплексного подхода
Из проведенных исследований можно сделать вывод о цикличности эксперимента. Количество таких экспериментов будет зависеть от уровня детализации факторов, влияющих на качество продукции. Решение об остановке эксперимента принимает организация, которая определяет глубину декомпозиции.
Охрана труда
Поиск по сайту: