Энтропия. Энтропия – функция состояния термодинамической системы, используемая во втором законе т/д для выражения через нее возможности или невозможности

Энтропия – функция состояния термодинамической системы, используемая во втором законе т/д для выражения через нее возможности или невозможности самопроизвольного протекания процесса (введена Клаузиусом).

Изменение энтропии определяется отношением количества теплоты, сообщенного системе или отведенного от нее, к температуре системы:

,

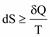где знак равенства относится к равновесному процессу, неравенства – к неравновесному.

Т.о. в равновесном процессе: S = .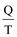

По изменению энтропии в изолированной системе можно предсказать т/д возможность протекания самопроизвольного неравновесного процесса. Если энтропия увеличивается (S > 0), то самопроизвольный неравновесный процесс возможен, если S < 0 – невозможен. Т.о. все самопроизвольные процессы в изолированных системах идут в сторону увеличения энтропии до достижения равновесия, где она будет иметь постоянное и максимальное значение.

В современной термодинамике второе начало термодинамики изолированных систем формулируется единым и самым общим образом как закон возрастания особой функции состояния системы, которую Клаузиус назвал энтропией (S).

Физический смысл энтропии состоит в том, что в случае, когда материальная система находится в полном термодинамическом равновесии, элементарные частицы, из которых состоит эта система, находятся в неуправляемом состоянии и совершают различные случайные хаотические движения.

В принципе можно определить общее число этих всевозможных состояний.

Параметр, который характеризует общее число этих состояний, и есть энтропия.

Рассмотрим это на простом примере.

Пусть изолированная система состоит из двух тел «1» и «2», обладающих неодинаковой температурой T ₁ > T ₂. Тело «1» отдает некоторое количество тепла Q, а тело «2» его получает. При этом идет тепловой поток от тела «1» к телу «2». По мере уравнивания температур увеличивается суммарное количество элементарных частиц тел «1» и «2», находящихся в тепловом равновесии.

По мере увеличения этого количества частиц увеличивается и энтропия. И как только наступит полное тепловое равновесие тел «1» и «2», энтропия достигнет своего максимального значения. Таким образом, в замкнутой системе энтропия S при любом реальном процессе либо возрастает, либо остаётся неизменной, т. е. изменение энтропии Δ S =0. Знак равенства в этой формуле имеет место только для обратимых процессов. В состоянии равновесия, когда энтропия замкнутой системы достигает максимума, никакие макроскопические процессы в такой системе, согласно второму началу термодинамики, невозможны.

Отсюда следует, что энтропия - физическая величина, количественно характеризующая особенности молекулярного строения системы, от которых зависят энергетические преобразования в ней.

Связь энтропии с молекулярным строением системы первым объяснил Л. Больцман в 1887 году. Он установил статистический смысл энтропии (формула 1.6). Согласно Больцману (высокая упорядоченность имеет относительно низкую вероятность)

где k — постоянная Больцмана, P – статистический вес.

k = 1.37·10^-23Дж/К.

Статистический вес Р пропорционален числу возможных микроскопических состояний элементов макроскопической системы (например, различных распределений значений координат и импульсов молекул газа, отвечающих определённому значению энергии, давления и других термодинамических параметров газа), т. е. характеризует возможное несоответствие микроскопического описания макросостояния.

Для изолированной системы термодинамическая вероятность W данного макросостояния пропорциональна его статистическому весу и определяется энтропией системы:

Таким образом, закон возрастания энтропии имеет статистически-вероятностный характер и выражает постоянную тенденцию системы к переходу в более вероятное состояние. Отсюда следует, что наиболее вероятным состоянием, достижимым для системы, является такое, в котором события, происходящие в системе одновременно, статистически взаимно компенсируются.

В связи с этим, введена ещё одна функция –

ΔG – изобарно-изотермический потенциал (Энергия Гиббса) или свободная энергия Гиббса:

ΔG = ΔH – TΔS

где ΔH – изменение энтальпии, Т – абсолютная температура, ΔS – изменение энтропии.

Если ΔG <0, процесс протекает самопроизвольно (экзэргонический процесс), если ΔG > 0, то процесс невозможен (эндэргонический процесс).

ΔG <0, если ΔH<0, т.е. реакция экзотермическая, или ΔН > 0, но по абсолютной величине меньше T · ΔS (энтропийного фактора). Значение T · ΔS резко возрастает при высокой температуре и определяет направленность процесса. Этим объясняется изменение направленности некоторых реакций с повышением температуры.

Поиск по сайту: