ТЕОРИЯ СИЛЬНЫХ ЭЛЕКТРОЛИТОВ

Эта теория была создана в 1923 г Дебаем и Хюккелем. Поскольку в растворе сильные электролиты практически полностью диссоциируют на ионы, постольку в растворе резко увеличивается концентрация частиц (ионов), Þ расстояние между ними резко снижается и усиливается кулоновское взаимодействие между ионами.

Согласно закону Кулона сила притяжения или отталкивания между ионами равна:

F = Z₁Z₂/(er²),

где Z₁ , Z₂ – заряды ионов, r – расстояние меж ними, e - диэлектрическая проницаемость.

Кулоновским взаимодействием пренебречь нельзя, что делала теория Аррениуса. Поэтому законы, выведенные для слабых электролитов, оказались не действительны для сильных электролитов. Вследствие этого было введено понятие АКТИВНОСТИ. Активность – это действительная концентрация, которая может быть равна концентрации в разбавленных растворах, а в концентрированных - может изменяться в большую или меньшую сторону. Активность связана с концентрацией уравнением:

,

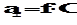где f – коэффициент активности изменяется в зависимости от концентрации.

При f = 1, а = С (в разб. Р-рах)..

Причем оказалось, что коэффициент активности сам весьма сложно зависит от концентрации (рис. 1).

Рис. Зависимость коэффициента активности электролита от его концентрации

В области низких концентраций (заштрихованная область) f = 1, а = С. На дальнейшем участке кривой f¹ 1 (концентрированные растворы), а ход кривой зависит от природы электролита, ионов, природы растворителя и др.

KA«K⁺ + A^-, , то правильно записать .

В этом уравнении принимает участие не концентрация вещества, а его активность.

В 1929 Хюккель показал, что определить активность или коэффициент активности в растворе отдельного иона нельзя, а коэффициент активности можно определить экспериментально в целом. Он равен из произведения коэффициентов активности катиона и аниона.

.

Существует параметр, позволяющий определить коэффициент активности, который называют ионной силой раствора :

,

С_i – молярная концентрация i-того иона, а z_i– его заряд.

[m] = моль×л^–1×кул²

Физический смысл ионной силы раствора: она характеризует суммарную величину электрического поля, образованного всеми ионами раствора, на произвольно выбранный ион в этом растворе.

Задача:

Вычислить ионную силу раствора, в 1 литре которого находится 0,1 моль Ba(NO₃)₂ и 0,2 моль KCl.

,

Ba(NO₃)₂ «Ba²⁺+ ; KCl«K⁺ + Cl^-

.

Если ионная сила находится в пределах 0,6 – 0,8 – это растворы средней концентрации, если менее 0,6 – разбавленные, если более 0,8 – концентрированные.

Ионная сила раствора позволяет определить коэффициент активности. В разбавленных растворах с концентрацией C£ 10^-3 моль/л Дебай предложил уравнение:

В общем виде: , Z – заряд иона, В – коэффициент (из таблицы), при 25⁰С он равен 0,5. При более высоких или низких температурах коэффициент может меняться.

Первое приближение Дебая для разб. растворов.

Для растворов средней силы им предложено второе приближение (концентрация более 10^-2 моль/л.:

Второе приближение Дебая.

Для еще более концентрированных растворов (С£5×10^–2 моль/л) Дэвис вывел уравнение:

- уравнение Дэвиса.

Задача. Рассчитать ионную силу и концентрацию ионов в 0,5 М растворе BaCl₂.

BaCl₂ «Ba⁺ + 2Cl^-

m = ½ (0,5∙2² + 1∙1²) = 1,5.

Рассчитать коэффициент активности и активность ионов.

С(Zn(NO₃)₂ = 0,05 M. Используя первое и второе приближение Дебая, получим:

и .

Zn(NO₃)₂ «Zn ²⁺ + m = ½ (0,05∙2² + 0,1∙1²) = 0,15.

а (Zn²⁺) = 0,17∙0,05 = 0,0085.

;

;

;

. ;

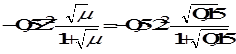а (Zn²⁺) = 0,276∙0,05 = 0,014.

; ;

.

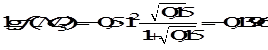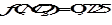Исходя из методов Дебая, коэффициент активности не зависит от природы ионов, т.к. в этих уравнениях используется заряд ионов и ионная сила, связанная с концентрацией. Таким образом, эти уравнения не учитывают природу ионов.

Поиск по сайту: