 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Обработка результатов наблюдений и оценка погрешности измерения
11.7.1 Метод взвешивания
При взвешивании будем использовать метод прямого противопоставления с внесением поправок на отклонение массы накладных гирь и на отклонение результата измерений из-за действия выталкивающей силы.
11.7.2 Порядок выполнения работы
11.7.2.1 Зафиксировать показание ненагруженных весов.
11.7.2.2 Поместить изделие, массу которого необходимо измерить, на левую чашку весов.
11.7.2.3 Помещая накладные гири на правую чашку весов и используя встроенные гири, добиться показания весов в пределах шкалы.
11.7.2.4 Зафиксировать значения массы использованных накладных ( ) и строенных гирь (
) и строенных гирь ( ).
).
11.7.2.5 Зафиксировать значение погрешности каждой используемой накладной гири (dгi), вычисляя его как разность между номинальным и действительным значением каждой гири. Действительное значение массы гирь должно быть установлено в результате поверки и регламентировано в свидетельстве о поверке.
11.7.2.6 Зафиксировать значение плотности материала (rх), из которого изготовлено изделие.
11.7.2.7 Результат измерения массы изделия вычислить по формуле (11.1):
 , (11.1)
, (11.1)
где а – масса взвешиваемого объекта;
аНгi – номинальное значение массы i-ой используемой накладной гири, г;
аВгi – номинальное значение массы i-ой используемой встроенной гири, г;
n – число использованных гирь;
Пri- поправка на погрешность i-ой используемой накладной гири, г; (равна значению погрешности i-ой используемой накладной гири dгi с обратным знаком);
Пη - поправка на погрешность из-за действия выталкивающей силы, г.
11.7.2.8 Границы погрешности измерения масс изделия при вероятности 0,95 оценить по формуле (11.2):
 , (11.2)
, (11.2)
где  – математическое ожидание погрешности измерения массы изделия из-за действия выталкивающей силы;
– математическое ожидание погрешности измерения массы изделия из-за действия выталкивающей силы;
σ дгi – среднее квадратическое отклонение (СКО) погрешности из-за неточности определения действительной массы i-ой используемой накладной гири;
σВг– СКО погрешности, встроенных гирь;
σн– СКО погрешности из-за неравноплечести весов;
σсл– СКО случайной составляющей погрешности весов;
σс– СКО погрешности измерения массы по шкале;
σшч– СКО погрешности считывания;
ση– СКО погрешности из-за действия выталкивающей силы (методическая погрешность).
11.7.3 Оценивание составляющих погрешности
11.7.3.1 Погрешность из-за неточности определения массы накладной гири
Действительное значение массы гирь устанавливается при аттестации сличением образцовой гирей или калибровкой набора по одной исходной образцовой гире. Погрешность аттестации  зависит от погрешности образцовых весов, от погрешности образцовой гири и погрешности определения поправки на действие выталкивающей силы. Значение погрешности аттестации используется для вычисления СКО погрешности из-за неточности определения действительной массы накладной гири (формула (11.3)):
зависит от погрешности образцовых весов, от погрешности образцовой гири и погрешности определения поправки на действие выталкивающей силы. Значение погрешности аттестации используется для вычисления СКО погрешности из-за неточности определения действительной массы накладной гири (формула (11.3)):
 (11.3)
(11.3)
11.7.3.2 Погрешность из-за неравноплечности коромысла
Даже при самой тщательной подгонке не удаётся добиться полной равноплечести коромысла. Остаточная неравноплечесть всегда имеет место и влияет на тонность результатов измерения. Допускаемые значения погрешности из-за неравноплечести весов регламентированы в документации на весы. Фактически значения погрешности индивидуальны для каждого вида весов и указываются в свидетельстве о поверке. Но их нельзя принимать в виде поправки, так как они определены при полной нагрузке и зависят от неё, а также из-за влияния ряда других факторов, среди которых основным является температура, значение погрешности будут изменяться, но не выйдут за пределы допускаемого значения. Поэтому СКО погрешности измерения будет вычисляться по формуле (11.4):
 , (11.4)
, (11.4)
где δн – допустимое значение погрешности из-за неравноплечести регламентированное в документации на весы;
1,2 – коэффициент для Р = 0,95 и антимодального распределения погрешности.
11.7.3.3 Погрешность включений встроенных гирь
Применение встроенных гирь вызывает погрешность измерения, допускаемое значение которой регламентировано в документе на весы. СКО этой составляющей вычисляется по формуле (11.5):
 , (11.5)
, (11.5)
где δВг – допустимое значение погрешности включений встроенных гирь, регламентированное в документации на весы.
11.7.3.4 Случайная составляющая погрешности
Случайная погрешность весов определяется вариацией показаний (размахом). Значение вариации установлено по результатам экспериментальных исследований и регламентировано в документации на весы (Dу). СКО случайной погрешности весов вычисляется по формуле (11.6):
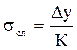 , (11.6)
, (11.6)
где К – коэффициент, зависящий от числа наблюдении при экспериментальном определении размаха. Например, n=3, К=1,67; n=5, К=2,33.
Для уменьшения случайной погрешности весов нужно увеличить число наблюдений (n). СКО случайной составляющей уменьшится при этом в  раз.
раз.
11.7.3.5 Погрешность измерения массы по шкале
Наличие шкалы у весов позволяет не производить уравновешивание до средней отметки шкалы и, тем самым, экономить время на выполнении измерений. Однако при этом возникает погрешность измерения массы по шкале, которая является следствием ошибок в расчёте, дефектов изготовления или неправильной установки шкалы. Значение этой погрешности регламентировано в документе на весы (dш). СКО погрешности измерения массы по шкале вычисляется по формуле (11.7):
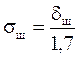 , (11.7)
, (11.7)
где δш– допустимое значение погрешности измерений по шкале, регламентированное в документации на весы
11.7.3.6 Погрешность считывания
При снятии отсчётов по шкале всегда имеет место погрешность считывания, которая зависит от цены деления шкалы. Значение СКО этой погрешности вычисляется по формуле (11.8):
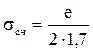 , (11.8)
, (11.8)
где е – цена деления шкалы, регламентированная в документации на весы
11.7.3.7 Методическая погрешность
При измерении массы источниками возникновения методической погрешности могут быть специфические свойства объекта измерения, изменение внешних условий. Обычно наиболее существенной является погрешность из-за действия выталкивающей силы. Её возникновение объясняется законом Архимеда, в соответствии с которым, на всякое тело, погруженное в жидкость или газ, действует выталкивающая сила, обратная по направлению силе тяжести и равная произведению объёма погруженной части тела на плотность окружающей жидкости или газа. Эта сила действует на груз и на гири. Так как груз и гири полностью погружены в воздух, то выталкивающая сила, действующая на груз  , а выталкивающая сила, действующая на гири
, а выталкивающая сила, действующая на гири  . Таким образом, действие выталкивающей силы определяется разностью объёмов груза и гирь. Это значит, что если сравнить на весах две гири одинаковой массы, но изготовление, например, из латуни и стали, то латунная гиря в воздухе перевесит стальную, то есть действие аэростатической силы зависит от плотности взвешиваемых изделий (rх) и гирь (rг).
. Таким образом, действие выталкивающей силы определяется разностью объёмов груза и гирь. Это значит, что если сравнить на весах две гири одинаковой массы, но изготовление, например, из латуни и стали, то латунная гиря в воздухе перевесит стальную, то есть действие аэростатической силы зависит от плотности взвешиваемых изделий (rх) и гирь (rг).
Значение поправки  вычислить по формуле (11.9):
вычислить по формуле (11.9):
 , (11.9)
, (11.9)
где rв – плотность воздуха при нормальных условиях (температура 20 °С, давление 101, 8 кПа), rв =1,2*10-3 г/см3;
rх – номинальная плотность материала изделия, масса которого измеряется, г/см3 ;
rг – условная плотность материала гирь, г/см3 .
Погрешность определения поправки из-за влияния выталкивающей силы, которое определяется отклонением плотности груза от её номинального значения, отклонением плотности воздуха в реальных условиях измерений от её значения в нормальных условиях и отличием массы груза от массы гирь. В соответствии с этим характеристики определения поправки на действие выталкивающей силы вычисляются по формулам (11.10),(11.11):
 , (11.10)
, (11.10)
 , (11.11)
, (11.11)
где  - математическое ожидание погрешности определения поправки;
- математическое ожидание погрешности определения поправки;
ση – СКО погрешности определения поправки;
σρх – СКО погрешности определения поправки из-за отклонения плотности груза от её номинального значения, г;
аг – сумма номинальных значений масс использованных накладных и встроенных гирь, г.
Значение СКО вычисляется по формуле (11.12):
 , (11.12)
, (11.12)
где δρх – допускаемое отклонение плотности груза, регламентированное в документации на материал груза или указанное в справочной литературе, г
σρв– СКО погрешности определения поправки из-за отклонения воздуха в реальных условиях от её значения в нормальных условиях. Для вычисления рекомендуется использовать значение  г/см3
г/см3
Результат записывается в виде:
А= 
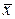 ±σ,
±σ,
где среднее арифметическое находим по формуле (11.13):
 (11.13)
(11.13)
где n - количество измерений;
х i - совокупность значений случайной величины;
11.7.4 Оценка составляющих погрешности измерений по РМГ 29-99
При статистической обработке результатов наблюдений выполняют следующие операции:
- вычисление среднего арифметического исправленных результатов наблюдений, принимаемых за результат измерения;
- оценки среднеквадратического отклонения (СКО) результата измерения доверительных границ случайной составляющей погрешности результата измерений;
- исключение систематические погрешности результата измерений и погрешности результата измерения;
- внесение вычислительных поправок в результат измерений.
Несмещенную оценку для СКО определяют по формуле (11.14):

 (11.14)
(11.14)
где 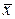 - среднее арифметическое результатов наблюдения
- среднее арифметическое результатов наблюдения
xi - i-ый результат наблюдения.
Случайную погрешность считают пренебрежительно малой величиной по сравнению с неисключенным остатком систематической погрешности (НСП), если обеспечивается неравенство (11.15):
Θ(Ρ)/S(x)≥8, (11.15)
Тогда доверительная граница погрешности вычисляется по формуле (11.16):
 , (11.16)
, (11.16)
Неисключенная систематическая погрешность определяется по формуле в соответствии с РМГ 29 – 99 «Рекомендации по межгосударственной стандартизации. Метрология. Основные термины и определения».
 (11.17)
(11.17)
где Θi – граница i – ой не исключенной систематической погрешности.
Под границами неисключенной систематической погрешности понимают границы интервала, найденные нестатистическими методами, внутри которого находится неисключенная систематическая погрешность измерения.
Еще до начала расчёта результатов наблюдений систематические погрешности исключаются. После их исключения вводится поправка и включается в состав составляющих систематических погрешностей вместе с остальными неисключительными систематическими погрешностями (НСП). Для обнаружения НСП рекомендуется провести измерение другими методами, сменить оператора измерения, сменить время суток и т.п.
Если выполняется неравенство 0,8 ≤ Θ(Ρ)/S(x),, то неисключенной систематической погрешностью пренебрегают и принимают в качестве погрешности результата измерения доверительные границы случайных погрешностей:
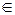 (Р)= Z (P/2) · S(x) (11.18)
(Р)= Z (P/2) · S(x) (11.18)
где Z(Р/2) - точка нормированной функции Лапласа;
S(х) - оценка средне квадратического отклонения
Если 0,8 < Θ(Ρ)/S(x) < 8, то доверительную границу погрешности результата измерений вычисляют по ниже приведенным формулам:

 , (11.19)
, (11.19)
 , (11.20)
, (11.20)
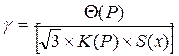 . (11.21)
. (11.21)
Результат записывается в виде:
А= х±ΔР
Поиск по сайту: