АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Опр. 3

Отображение f: X 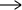Y имеет обратное отношение f -1: Y 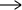X тогда и только тогда, когда f – биекция.

Если f – биекция, то, поскольку f – сюръективно, f -1 определено на множестве Y. Кроме того, f – функция, так как если <y, x1> f -1 и <y, x2> f -1, то <x1, y> f и <x2, y> f, то в силу инъективности f имеем x1 = x2.

Пусть теперь отображение f имеет обратное отображение f -1, определенное на множестве Y со значениями во множестве X. Тогда f – сюръективно, поскольку для 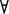у Y прообраз x X. при этом f – инъективно, так как если <x1, y> f и <x2, y> f, то <y, x1> f -1 и <y, x1> f -1, а так как f -1 – функция, то x1 = x2.

Свойства инъективных функций f и g.

1. (f -1)-1 = f

2. (g f)-1 = f -1 g -1

Если f: X Y – биекция, то

3. (f -1 f) = ex

4. (f f -1) = ey


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)