 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Опр. 1
(о приведении к ДНФ). Для любой формулы А можно найти такую формулу В, находящуюся в ДНФ, что А 
В.
1. Для формулы А строим такую формулу А1, что в А1 не содержится элементов 
или ~.
2. Пусть 
А2 А1, причем отрицание в этих формулах содержится только перед переменными.
Тогда пусть n, т.е количество логических символов в некой формуле. Если n =0, то А1 это переменная Х. тогда в качестве А2 нужно взять Х. Утверждение выполняется для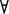 
формулы, где кол-во символов меньше n. пусть А1 где колво элементов равно n. Тогда:
1) А1 имеет вид С1 
В1. Тогда в В1 и С1 логических символов меньше n. Поэтому формулы В2 С2, такие, что С1 = С2, а В1 = В2 и в В2 С2 отрицание встречается только перед переменными. Очевидно, что С2 В2 равносильна А1.
2) А1 имеет вид С1 
В1. Доказательство аналогично.
3) А1 имеет вид 
В1. Тогда А1 В1 и в В1 логических символов меньше, чем n. поэтому к В1 применимо индуктивное предположение.
4) А1 имеет вид (В1 С1). Тогда А1 В1 С1 и В1, С1 логических символов меньше, чем n. Поэтому такие В2 и С2, что В1 В2, С1 В2, и в В2, С2 отрицание встречается только перед переменными. Ясно, что А1 В2 С2.
5) А1 имеет вид (В1 С1). Аналогично предыдущему.
На практике используются законы де Моргана.
3. Полученную формулу А2 можно считать построенной из переменных и их отрицаний. теперь можно использовать дистрибутивность относительно . При этом будет вести себя как умножение, а как сложение. Полученная формула В будет удовлетворять требованиям доказываемой теоремы.
Поиск по сайту: