Билет 27. «Основные понятия логики предикатов (ЛП)

«Основные понятия логики предикатов (ЛП). Формула, интерпретация».

Предикатом Р(х₁,…,х_n) называется функция, переменные которой принимают значения: истинное (И) или ложное (Л), т.е. Р(х₁,…,х_n): М_n 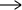{И, Л}. Предикат от n аргументов называется n-местным предикатом.

Если точки плоскости лежат на одной прямой, то это выражается предикатом L(x, y, z), где x, y, z – точки этой плоскости.

Пусть Р(х) – некоторый предикат, принимающий И или Л значения для каждого значения х на множестве М. тогда (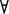 х)Р(х) будет выражать истинное высказывание для любого х на множестве М. в противном случае высказывание будет ложным. Здесь( 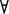х) это квантор общности.

Пусть Р(х) – некоторый предикат, принимающий И или Л значения для каждого значения х на множестве М. тогда ( х)Р(х) будет выражать истинное высказывание для некоторого х на множестве М. в остальных случаях высказывание будет ложным. Здесь( х) это квантор существования.

Алфавит логики предикатов:

1. Символы предметных переменных х₁, х₂,… (во избежание нагромождения индексов используются x y z)

2. Символы предикатов А^(t)₁, А^(t)₂,…; где t N

3. Логические символы , , ,…

4. Символы кванторов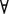

5. Скобки и запятые

Слово в алфавите логики называется формулой.

1. Пусть А –символ предиката, х, у – символы предметных переменных, тогда А(х, у) – атомарная формула.

2. Пусть А – формула. Тогда А – тоже формула.

3. Пусть А и В – формулы, при этом нет переменных, которые были бы связаны в одной формуле, а свободны в другой. Тогда

А В,…; где связанные и свободные переменные остаются неизменными.

4. Пусть А – формула, где переменная х –свободная, тогда (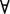 х)А – тоже формула, но переменная А в ней уже связана. Остальные переменные в А остаются свободными. Здесь А называется областью действия квантора.

Под интерпретацией понимают систему M = <M, f >, состоящую из непустого множества М и соответствия f, сопоставляющего каждому предикатному символу А^(t)_j t-местный предикат.

При интерпретации считают, что переменные пробегают множество М, а кванторы и логические символы остаются прежними. Значение формулы определяется на наборе <a₁,…,a_n>, где все а принадлежат множеству М. а значением формулы называется значением t-местного предиката при определенном замещении переменных значениями а. Результат обозначается буквой эпсилон.

Поиск по сайту: