Билет 29

«Приведенная нормальная форма формул ЛП. Алгоритм построения ПНФ с тождествами».

Приведенными формулами называются формулы, в которых из логических символов имеются только , и , причем символ встречается только перед символами предикатов.

Приведенная формула называется нормальной, если она не содержит символов кванторов или все символы кванторов стоят впереди.

1. Перенос квантора через отрицание. Пусть А – формула, содержащая св. переменную х. тогда справедливы равносильности:

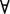( х)А(х) ( х) А(х) и наоборот.

Докажем равносильность. Пусть х_i1,…., x_in – множество всех свободных переменных формулы А, отличных от х. пусть М = <M, f > - произвольная интерпретация. Докажем, что на любом наборе значений своих свободных переменных <a₁, …, a_n>, a_i M, формулы принимают истинное значение.

Возможны 2 случая:

1) Для любого а М А(х)|_{<a, a1,…, an>} = И

2) Для некоторого а₀ М А(х)|_{<a0, a1,…, an>} = Л

Для первого случая для 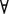а М: А(х)|_{<a, a1,…, an>} = Л. Отсюда по определению ( х) А(х)|_{<a1,…, an>} = Л. С другой стороны (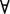 х)А(х)|_{<a1,…, an>} = И. Тогда ( 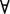х)А(х)|_{<a1,…, an>} = Л.

Во втором случае для элемента а₀ М: А(х)|_{<a0, a1,…, an>} = И. Отсюда ( х) А(х)|_{<a1,…, an>} = И. С другой стороны, в этом случае (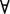 х) А(х)|_{<a1,…, an>} = Л. Отсюда ( 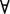х) А(х)|_{<a1,…, an>} = И. Равносильность доказана.

2. Вынос квантора за скобки. Пусть формула А(х) содержит свободную переменную х, формула В не содержит переменной х и обе удовлетворяют определению формул. Тогда

( х)(А(х) В) ( х)А(х) В

Докажем. (Оставшийся квантор и дизъюнкция раскрываются и доказываются аналогично). В обеих частях равенства свободные переменные <x_i1,…,x_in> сохраняются.

Рассмотрим произвольную интерпретацию с множеством М. Пусть <a₁, …, a_n>, а_i M – произвольный набор значений свободных переменных x_i1,…,x_in. Так как формула В не содержит переменной х, то можно определить значение этой формулы на наборе <a₁, …, a_n> (точнее, на его части, относящейся к свободным переменным формулы В). Если В|_{<a1,…, an>} = Л, то (( х)А(х) В)|_{<a1,…, an>} = Л, и для 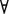а из множества М на наборе значений <а, a₁, …, a_n> свободных переменных х, x_i1,…,x_in формула А(х) В принимает значение Л. Отсюда ( х)(А(х) В)|_{<a1,…, an>} = Л. Если В_{<a, a1,…, an>} = И, то для 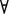а М на наборе <а, a₁, …, a_n> формулы А(х) В и А(х) принимают одинаковые истинностные значения. Отсюда (( х)А(х) В)|_{<a1,…, an>} = ( х)А(х) |_{<a1,…, an>} = ( х)(А(х) В)|_{<a1,…, an>}.

Если не требовать того чтобы переменная х не входила в В, то

( х)(А(х) В(х)) ( х)А(х) ( х)В(х).

3. Перестановка одноименных кванторов:

( у) ( х)А(х, у) ( х) ( у)А(х, у) (с другим квантором аналогично)

4. Переименование связанных переменных. Заменяя связанную переменную формулы А другой переменной, не входящей в эту формулу, в кванторе и всюду в области действия квантора получаем формулу, равносильную А. Доказывается методом индукции по длине.

Поиск по сайту: