Пример. Множество Z всех целых чисел имеет нумерацию

Множество Z всех целых чисел имеет нумерацию.

Нетрудно заметить, что все отрицательные числа нумеруются четными номерами, а неотрицательные – нечетными.

Свойства

1. Любое подмножество счётного множества не более чем счётно.

2. Пересечение счетных множеств счетно или конечно.

А

3. Объединение конечного или счётного числа счётных множеств счётно.

Доказывается матричным обходом.

4. Прямое произведение счетного числа счётных множеств не счётно.

5. Множество всех конечных подмножеств счётного множества счётно.

6. Любое бесконечное множество А содержит счетное подмножество В.

Билет 12.

«Теорема Кантора о несчетности точек отрезка [0, 1]».

[0, 1] – не равномощно N.

Опр.

Не существует взаимооднозначного соответствия между точками отрезка [0, 1].

Док-во. (от противного)

А вот допустим, что это не так.

Обозначим точки отрезка [0, 1]. a_i = 0, a_i1 a_i2 … [0, 1].

Итого:

1 a₁ = 0, a₁₁ a₁₂ …

2 a₂ = 0, a₂₁ a₂₂ …

k a₃ = 0, a₃₁ a₃₂ …

Итак, мы занумеровали точки отрезка. Однако:

b [0, 1], b = b₁ b₂ b₃ …

При этом b_i 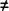ни нулю, ни единице, ни одному из a_ii. Таким образом, b нельзя занумеровать, потому что b отличается своими цифрами от a_ii.Поэтому нельзя занумеровать все точки отрезка, т.к обязательно найдется такое b,которое не будет совпадать с пронумерованными числами. Противоречие означает доказательство. Отрезок является несчетным.

Поиск по сайту: