 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Билет 7. «Функция. Инъективная, сюръективная и биективная функции
«Функция. Инъективная, сюръективная и биективная функции. Примеры».
Бинарное отношение f называется функцией, если из <x, y> 
f и <x, z> f следует, что y = z. Поскольку функции являются бинарными, то (по интуитивному принципу объемности), две функции f и g равны, если они состоят из одинаковых элементов. Область определения функции обозначается как Df, а область значений – Rf. Определяются они также как и для бинарных отношений.
Допустим, что Df = Х, а Rf 
Y, то функция задана на множестве Х со значениями во множестве Y, т.е f: X 
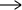Y.
Если f – функция, то вместо <x, y> f пишут y = f (x).
Поиск по сайту: