Опр. 1. Принцип двойственности. Пусть

Принцип двойственности. Пусть

Ф = f ₁(Х₁,…, Х_j-1, f ₂ (Х₁, …, Х_k2), X_j+1, …, Х_k1).

Тогда

Ф = f ₁^*(Х₁, …, Х_j-1, f ₂^* (Х₁, …, Х_k2), X_j+1, …, Х_k1).

Действительно, без ограничения общности можно считать, что k₁ > k₂. Тогда

Ф^*(Х₁, …, Х_k1) = Ф ( Х₁, …, Х_k1) = f ₁( Х₁, …, Х_j-1, f ₂ ( Х₁, …, Х_k2), X_j+1, …, Х_k1) = f ₁( Х₁, …, Х_j-1, f ₂^*(Х₁, …, Х_k2), X_j+1, …, Х_k1) = f ₁^*(Х₁, Х_j-1, f ₂^*(Х₁, …, Х_k2), X_j+1, …, Х_k1).

Функция f ₁(Х₁, …, Х_n) называется самодвойственной, если f ₁(Х₁, …, Х_n) = f ₁^*(Х₁, …, Х_n). Класс самодвойственных функций обозначается буквой S. Класс самодвойственных функций функционально замкнут. Это следует из утверждения выше, поскольку f ₁ f ₂ S (f ₁ = f ₁^*, а f ₂ = f ₂^*), то Ф = Ф^*. замена переменной также не выводит из S.

Функция f (Х₁, …, Х_n) называется линейной, если f (Х₁, …, Х_n) = а₀+а₁Х₁+ … + а_nХ_n L, где а_i {0, 1}. Класс линейных функций обозначается как L.

Класс линейных функций функционально замкнут. Пусть f ₁ = а₀+а₁Х₁+ … + а_k1Х_k1 L, а f ₂ = b₀+b₁Х₁+ … + b_k2Х_k2 L. Тогда а₀+… + а_j-1Х_j-1+ a_i(b₀+b₁Х₁+ … + b_k2Х_k2)+ a_j+1X_j+1+ … + а_k1Х_k1 L, что следует из правила равносильных преобразований. (Пусть С_а – некоторая формула. При замене вхождении А в эту формулу на вхождение В, получится формула С_в, причем, если А В, то С_а С_в)

Говорят, что оценка а = <a₁, …, a_n> предшествует оценке b = <b₁, …, b_n>, где a_i и b_i {0, 1}, i = 1, …, n, если a_i b_i для 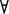i (или а b).

Поиск по сайту: